Предмет: Алгебра,
автор: arturpos123
Помогите пж!
Заранее спасибо!
Приложения:
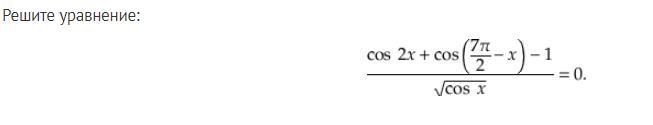
Ответы
Автор ответа:
0
Ответ:
Решить уравнение
ОДЗ:
По формуле приведения запишем
Теперь отберём корни, принадлежащие ОДЗ , получим ответ .
Ответ: .
Приложения:


Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Химия,
автор: lunaradarmedova
Предмет: Українська мова,
автор: solomiiamerzliak
Предмет: Английский язык,
автор: Pashok21rus
Предмет: Математика,
автор: utkelbaevaradmila5