Предмет: Алгебра,
автор: nick1991162
Помогите решить уравнение
Приложения:
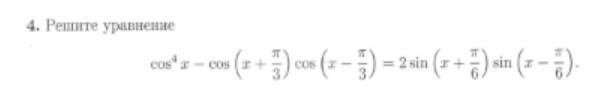
Ответы
Автор ответа:
0
Мы воспользуемся формулами
Похожие вопросы
Предмет: Українська мова,
автор: prohnitkaanna
Предмет: Английский язык,
автор: mohammadnahed393
Предмет: Українська мова,
автор: polinapersic28062012
Предмет: Русский язык,
автор: terkina0081
Предмет: Математика,
автор: popowaanaoxup93