Question

ПОМОГИТЕ ПОЖАЛУЙСТА
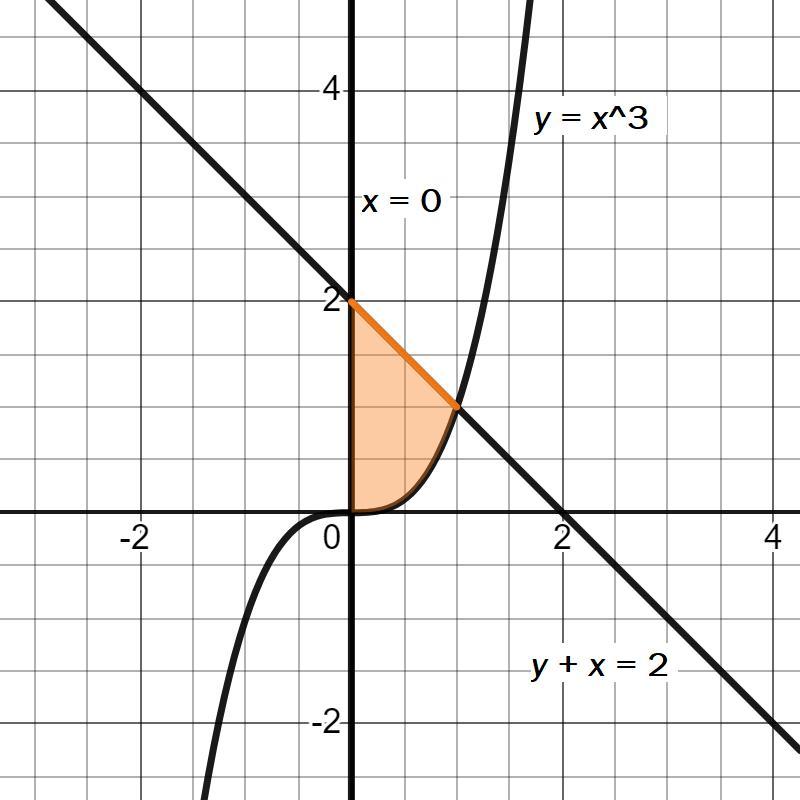
Вычислить двойной интеграл по области D: {{xdxdy, D: y = x³, x = 0, y + x = 2

Answer 1

Изобразим область $D$ (см. рисунок). Найдём границы интегрирования по, например, переменной $x$.

$y = x^3,\, y= 2 -x \implies x^3 + x - 2 = 0 \iff (x-1)(x^2+x+2) = 0\iff x = 1.$

То есть,

$\displaystyle \begin{aligned}\iint_D x\,\mathrm{d}x\,\mathrm{d}y &= \int_0^1 x\,\mathrm{d}x\int_{x^3}^{2-x}\mathrm{d}y = \int_0^1 x\big(2-x-x^3\big)\,\mathrm{d}x = \\[2ex] &=\bigg(x^2-\frac{x^3}{3} - \frac{x^5}{5}\bigg)\Bigg|_{0}^{1} = \frac{7}{15}.\end{aligned}$

Ответ. $\tfrac{7}{15}$