Предмет: Алгебра,
автор: sw3toff
Даю 100 баллов. Розв’язати диференціальне рівняння
Приложения:
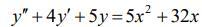
ГАЗ52:
https://znanija.com/task/25654883
Ответы
Автор ответа:
1
Ответ:
Решить ЛНДУ 2 пор. с постоянными коэффициентами .
( ЛНДУ - линейное неоднородное диффер. уравнение ) .
Общее решение ЛОДУ 2 пор. : .
По виду правой части уравнения запишем вид частного решения ЛНДУ 2 пор.
Найдём коэффициенты с помощью метода неопределённых коэффициентов .
Запишем частное решение ЛНДУ 2 пор. :
Общее решение ЛНДУ 2 пор. :
Приложения:


Автор ответа:
0
Данное дифференциальное уравнение решается довольно просто через преобразование Лапласа
- это константы, мы пока их оставим, мало ли сократятся
Теперь нам нужно найти обратное преобразование лапала этого выражения
Теперь мы получаем решение
Похожие вопросы
Предмет: Алгебра,
автор: Violetta856
Предмет: Геометрия,
автор: popl30612
Предмет: Английский язык,
автор: Mamaamakriminal22
Предмет: Математика,
автор: Damia9
Предмет: Литература,
автор: kondrashova10