Предмет: Алгебра,
автор: sw3toff
Даю 100 баллов. Розв’язати диференціальне рівняння з відокремлюваними змінними
Приложения:
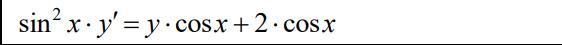
Ответы
Автор ответа:
1
Перепишем наше уравнение, то есть поделим всё на
Умножим всё на и поделим на
, получаем
Похожие вопросы
Предмет: Математика,
автор: lytaivika23
Предмет: Физика,
автор: bagdasariankhoren11
Предмет: Физика,
автор: starlightmeow
Предмет: Геометрия,
автор: NYASHA525
Предмет: Математика,
автор: fantasylook515