Предмет: Алгебра,
автор: sw3toff
Даю 100 баллов. Знайти невизначені інтеграли
Сделать надо 2,5,11,12
Приложения:
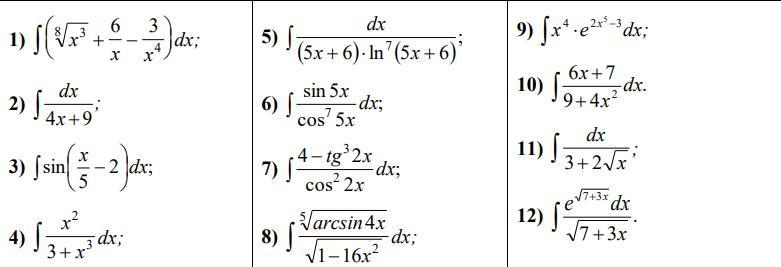
Ответы
Автор ответа:
1
sw3toff:
Благодарствую
Похожие вопросы
Предмет: Физика,
автор: dldlldlld
Предмет: История,
автор: alinadvor1985
Предмет: Алгебра,
автор: matvijeremenko
Предмет: Математика,
автор: Tatiana963963