Question

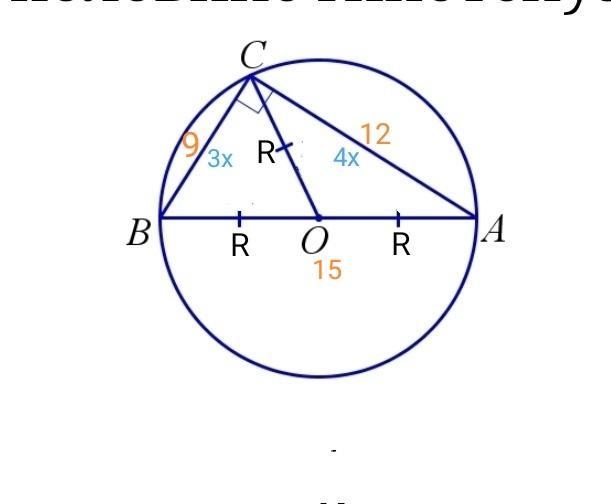
В треугольнике ABC угол С равен 90°, BC= 9, tgA=3/4 Найдите радиус окружности, описанной около треугольника ABC.​

Answer 1

Ответ:

7,5.

Пошаговое объяснение:

Первый способ решения:

1. В прямоугольном ∆ АВС по условию ∠С = 90°, тогда ∠А острый.

2. 1 + ctg²A = 1/(sin²A)

sin²A = 1/(1 + ctg²A)

По условию tg A = 3/4, тогда

ctgA = 1/tgA = 4/3 и

sin²A = 1/(1 + 16/9) = 1/(25/9) = 9/25.

Т.к. ∠А острый, то sinA > 0,

sin A = +√(9/25) = 3/5.

3. По теореме

R = a/(2•sinA) = BC/(2•3/5) = 9•5/(1•6) = 15/2 = 7,5.

Ответ: 7,5.

Второй способ решения:

1. В прямоугольном треугольнике АВС ( ∠ C = 90°) по определению

tg A = BC/AС = 3/4.

Пусть длина одной части равна х , тогда

ВС = 3х = 9,

х = 3, тогда АС = 4х = 4•3 = 12.

2. По теореме Пифагора

АВ² = АС² + ВС² = 12² + 9² = 225,

АВ = √225 = 15.

3. В прямоугольном треугольнике центром описанной окружности является середина гипотенузы, тогда

R = c/2 = AB/2 = 15/2 = 7,5.

Ответ: 7,5.



Answer 2

Відповідь: 7,5

##################