Помогите пожалуйста, даю 100 баллов
нужно решить через теорему Пифагора

Ответы
Ответ:
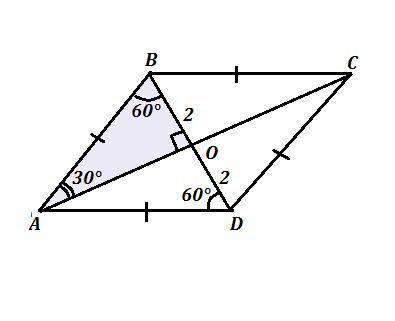
Дан ромб ABCD ⇒ АВ=ВС=CD=AD и BD ⊥ AC , BD=4 см
Диагонали в точке пересечения делятся пополам, то есть ВО=DO=2 см , АО=СО .
Значит треугольники АВО , ВСО , CDO , АВО - прямоугольные . Они ещё и равные по двум катетам , так как катетами этих треугольников служат половинки диагоналей .
Угол между BD и АВ равен 60° , то есть ∠ABD = 60° , а значит в прямоугольном треугольнике АВО угол ∠ВАО=30° . А против угла в 30° лежит катет, равный половине гипотенузы , значит
ВО=1/2 · АВ и АВ = 2·ВО = 2 · 2 = 4 (см) .
Если надо решить через теорему Пифагора, то можно найти АО из треугольника АВО, применив эту теорему :
АВ² = АО² + ВО² ⇒ АО² = АВ² - ВО² = 4² - 2² = 16 - 4 = 12 , АО = √12
Тогда вторая диагональ ромба равна АС = 2 · АО = 2√12 = 4√3 см
Площадь ромба равна полупроизведению диагоналей .
S = 1/2 · AC · BD = 1/2 · 4√3 · 4 = 8√3 (см³)
Периметр ромба равен сумме всех его сторон , то есть
Р = 4·4 = 16 (см)
P.S. 1) Если эту формулу для площади ромба не знаешь, то можно найти S ромба как сумму площадей 4-х равных прямоугольных треугольников :
S = 4 · S(ABO) = 4 · (1/2 · AO · BO) = 4 · (1/2 · 4 · 4√3) = 8√3 (см³) .
2) Легко заметить и доказать, что если малая диагональ ромба образует со стороной ромба угол в 60° , то ромб разделяется на два равных равносторонних треугольника ABD и BDC . И площадь ромба можно найти и без теоремы Пифагора, как удвоенную площадь равностороннего треугольника со стороной а = 4 .