Предмет: Алгебра,
автор: Sayori44
СРОЧНО!!!
выполнить задания 18,19,20 с решением
Приложения:
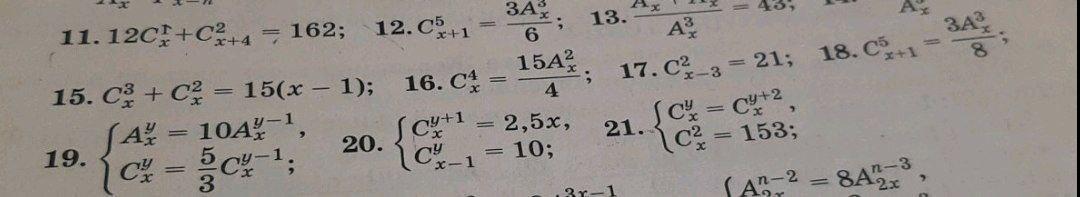
Ответы
Автор ответа:
0
Объяснение:
18.
ОДЗ: х+1≥5 х≥4.
Ответ: х=8.
19.
Упростим уравнение (1):
Упростим уравнение (2):
Ответ: х=15, у=6.
Похожие вопросы
Предмет: История,
автор: biblivivan9
Предмет: Українська мова,
автор: olggga123456789
Предмет: Химия,
автор: apssytnyk
Предмет: Русский язык,
автор: ArturKulichev
Предмет: Русский язык,
автор: ArturKulichev