Question

Різниця основ прямокутної трапеції дорівнює 9 см, а їїбічні сторони відносяться як 4:5. Знайдіть площу трапеції,якщо її менша діагональ дорівнює 13 см.

Answer 1

Ответ:     114 см².

Объяснение:

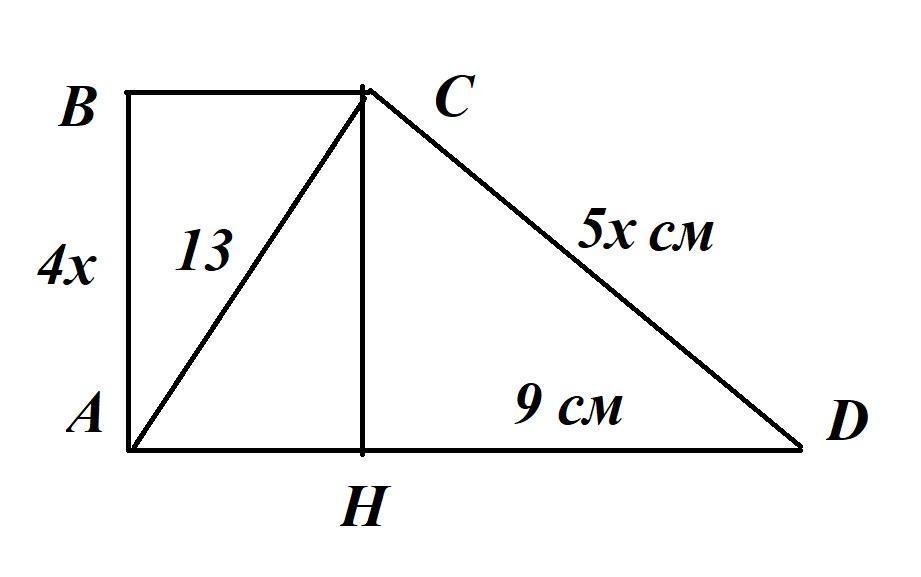
ABCD - трапеция.

Угол А равен углу В равен 90 градусов.

AC=13 см - меньшая диагональ.

AD-BC=9 см.

AB/CD = 4/5.

******************

Проведем высоту CH. По условию DH=9 см.

Пусть x - одна часть боковых сторон трапеции.  Тогда

AB=CH=4x см.  CD=5x см.

По т. Пифагора DH=√(5x)²-(4x)²) = 9;

√(25x²-16x²) = 9

√(9x²)=9

x=3  см.  Тогда

AB=CH=4x=4*3 = 12 см;

CD=5x=5*3=15 см.

BC=AH = √(AC²-AB²) = √(13²-12²) = √(169-144) = √25 = 5 см.

Так как AD-BC=9, то    AD=BC+9 = 5+9=14 см.

Площадь S(ABCD) = AB(BC+AD)/2 = 12(5+14)/2 = 6*19 = 114 см².