Question

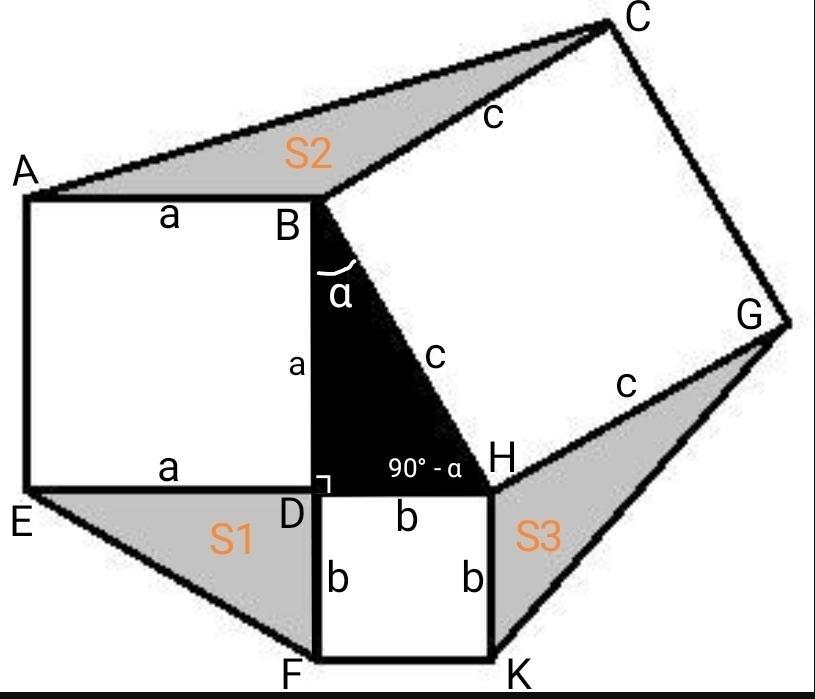
На сторонах прямоугольного треугольника построены квадраты («пифагоровы штаны»). Их вершины соединены так, как показано на рис. 1. Докажите равенство площадей серых треугольников.

Answer 1

Доказательство:

Пусть ∆ BDH - данный прямоугольный треугольник с катетами a и b и гипотенузой с, ∠DBH = α, тогда по теореме ∠DHВ = 90° - α.

По теореме площадь треугольника равна половине произведения двух его сторон на синус угла между ними, тогда

S BDH = 1/2•ac•sinα или

S BDH = 1/2•ab, или

S BDH = 1/2•bc•sin(90°-α) = 1/2•bc•cosα.

1. ∆ EDF прямоугольный с катетами a и b, тогда S1 = 1/2ab, т.е. S1 = S BDH.

2. Рассмотрим ∆ АВС:

∠АВС = 360° - (90° + 90° + α) = 180° - α.

S2 = 1/2 • a • c • sin∠ABC =

= 1/2•ac•sin(180°- α) = 1/2•ac•sinα, т.е.

S2 = S BDH.

3. Рассмотрим ∆ GHK:

∠GHK = 360° - (90° + 90° + 90° - α) = 90° + α,

S3 = 1/2 • b • c • sin(90° + α) = 1/2•bc•cosα, т.е. S3 = S BDH

Итак, получили, что площадь каждого серого треугольника равна площади первоначально данного ∆ BDH, поэтому равенство площадей всех серых треугольников доказано