Предмет: Математика,
автор: prawn05
Плииз помогите решить
Приложения:

liftec74:
Я решил 6 и 7. 8 решать пока нет времени. Ответы 2) и 2). Поместите пож все вопросы отдельно. Писать сразу 3 нет сил.
Ответы
Автор ответа:
0
Ответ:
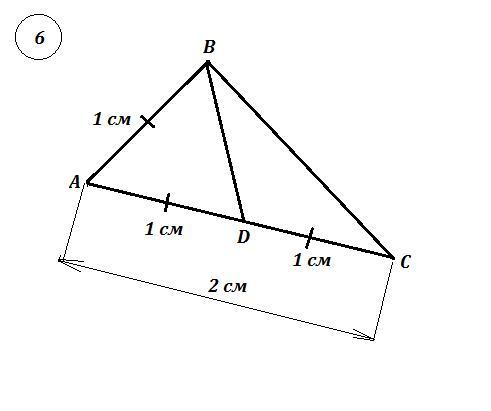
6) ΔАВС , АВ=1 см , АС=2 см , BD - медиана : AD=DC , BD=√3 см .
Найти S(ABC) .
Медиана делит треугольник АВС на два равновеликих треугольника , поэтому S(ABC) = S(ABD) + S(BDC) = 2 ·S(ABD) .
Найдём S(ABD) , зная три стороны этого треугольника : АВ=1 см , AD=AC : 2 = 1 см , BD=√3 cм .
Можно найти площадь по формуле Герона . А можно вычислить sin∠A и применить формулу площади треугольника S = 0,5· a · b · sinα
По теореме косинусов .
Наименьшее целое решение неравенства .
Ответ: .
Корни, принадлежащие промежутку :
Ответ: 5 корней .
Приложения:
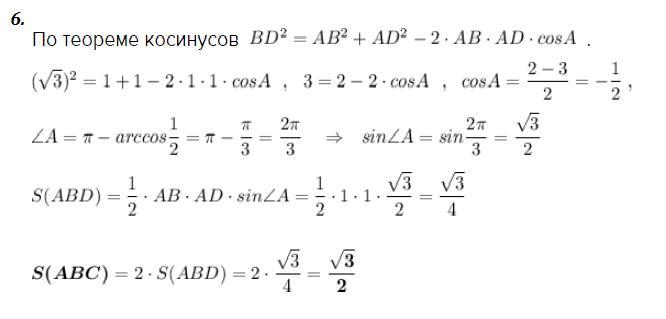



Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: История,
автор: 29yemarchuk
Предмет: История,
автор: lisenkoandrij6
Предмет: Музыка,
автор: 837393939392920
Предмет: Математика,
автор: Spookeysus