Предмет: Геометрия,
автор: apologojko
Помогите , завдання на фото
Приложения:

ГАЗ52:
а) Катеты прямоугольного треугольника равны 6 см и 8 см. Найти площадь треугольника, вершины которого середина медианы к гипотенузе и концу большего катета.
Ответы
Автор ответа:
1
Ответ:
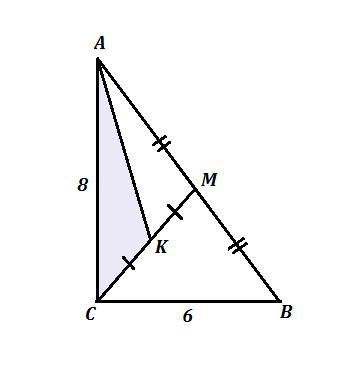
Дан ΔАВС , ∠С=90° , АС=8 см , ВС=6 см .
СМ - медиана ⇒ АМ=ВМ , точка К - середина СМ , то есть СК=КМ .
Найти площадь ΔACK .
Свойство медианы треугольника : медиана разбивает треугольник на два равновеликих треугольника ,то есть на два треугольника с одинаковой площадью .
S(ABC) = 1/2 · AC · ВС = 1/2 · 8 · 6 = 24 (см²) .
СМ - медиана ⇒ S(ACM) = S(BCM) = 1/2 · S(ABC) ,
S(ACM) = 1/2 · 24 = 12 (см²)
Рассмотрим ΔАСМ , СК=КМ ⇒ АК - медиана треугольника АСМ ⇒
S(ACK) = S(AMK) = 1/2· S(ACM) , S(ACK) = 1/2 · 12 = 6 (см²)
Приложения:
Похожие вопросы