Предмет: Математика,
автор: andrejbaza26
Знайти похідну функції логарифмічним диференціюванням.
Приложения:

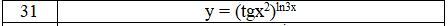
Ответы
Автор ответа:
1
Ответ:
Логарифмическое дифференцирование
Прологарифмируем уравнение , получим
Найдём производную от правой и левой частей уравнения.
Заменим теперь у на заданную функцию .
Аналогично решаем второй пример .
Приложения:

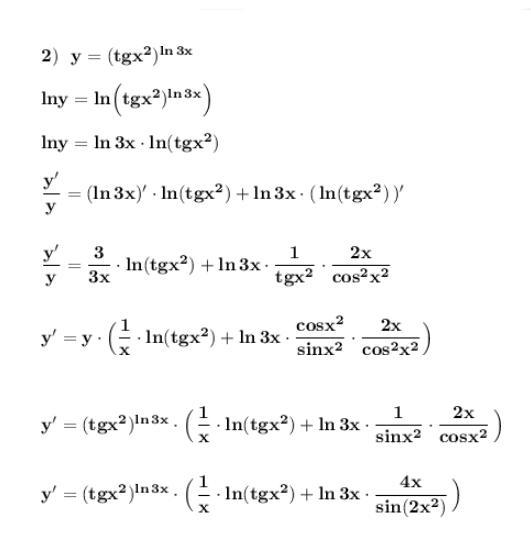
Похожие вопросы
Предмет: Алгебра,
автор: ruikamishiro1024
Предмет: Математика,
автор: MiKIozz
Предмет: Литература,
автор: anastasia240311
Предмет: Обществознание,
автор: nika2758