Здравствуйте, помогите пожалуйста с решением!
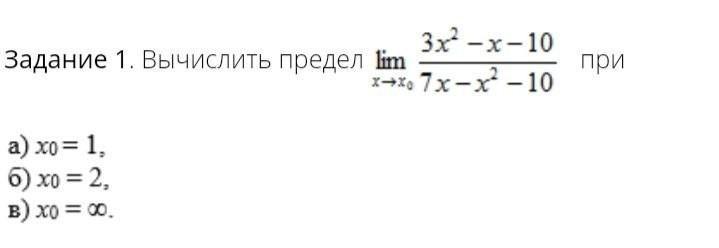
Ответы
Чтобы вычислить предел, нужно подставить число, к которому оно стремится
Изначальный вид предела:
Вместо х₀ мы будет подставлять значения, которые даны ниже
А
Б
Получили неопределенность вида , значит нам нужно разложить числитель и знаменатель:
Снова неопределенность, значит пробуем преобразовать еще раз. Факторизуем числитель и знаменатель:
В
Получили неопределенности вида , значит нужно разложить числитель и знаменатель:
Про неопределенности
Почему же и
являются неопределенностями?
В случае с нулем, мы знаем, что если 0 разделить на любое число, получим 0. Но при делении любого числа на 0, получается бесконечность. Отсюда и неопределенность. Вроде бы должны получить 0, но вроде и бесконечность
В случае же с бесконечностью, нельзя сказать, где она увеличивается быстрее, в числителе или знаменателе. Условно, бесконечность в числителе может начинаться от -1 и расти вверх, а в знаменателе от 1 и расти вверх. Или вообще одна из бесконечностей будет постоянно увеличиваться, а вторая бесконечно уменьшаться. Снова нельзя сказать, какой результат получим