Найдите такие числа M и N, чтобы выполнялось равенство(фото ниже)
если не тяжело, то с подробным решением ^@+@^
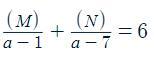
Ответы
Ответ:
вот всё в подробностях)
Для нахождения чисел M и N, чтобы выполнялось равенство (M)/(a - 1) + (N)/(a - 7) = 6, мы должны использовать данное уравнение и решить его относительно M и N.
Уравнение: (M)/(a - 1) + (N)/(a - 7) = 6
Для начала, мы можем умножить обе части уравнения на (a - 1)(a - 7), чтобы избавиться от знаменателей:
(M)(a - 7) + (N)(a - 1) = 6(a - 1)(a - 7)
Раскроем скобки:
Ma - 7M + Na - N = 6(a² - 8a + 7)
Приведем подобные члены:
(M + N)a - 7M - N = 6a² - 48a + 42
Теперь у нас есть уравнение, которое должно выполняться для любого значения a. Чтобы найти числа M и N, мы должны сравнить коэффициенты при a в обеих частях уравнения.
Сравнивая коэффициенты при a, мы получаем систему уравнений:
M + N = 0 (коэффициенты при a)
-7M - N = -48 (коэффициенты без a)
Решая эту систему уравнений, найдем значения M и N.
Умножим первое уравнение на -1 и сложим с вторым уравнением:
-7M - N - (M + N) = -48 - 0
-8M = -48
Делим обе части на -8:
M = -48 / -8
M = 6
Подставляем найденное значение M в первое уравнение:
6 + N = 0
N = -6
Таким образом, числа M и N, для которых выполняется равенство (M)/(a - 1) + (N)/(a - 7) = 6, равны M = 6 и N = -6.
M + N = 0 (коэффициенты при a)
-7M - N = -48 (коэффициенты без a)"