Предмет: Математика,
автор: markshunami
Дослідіть збіжність невласних інтегралів 2-го роду
Приложения:
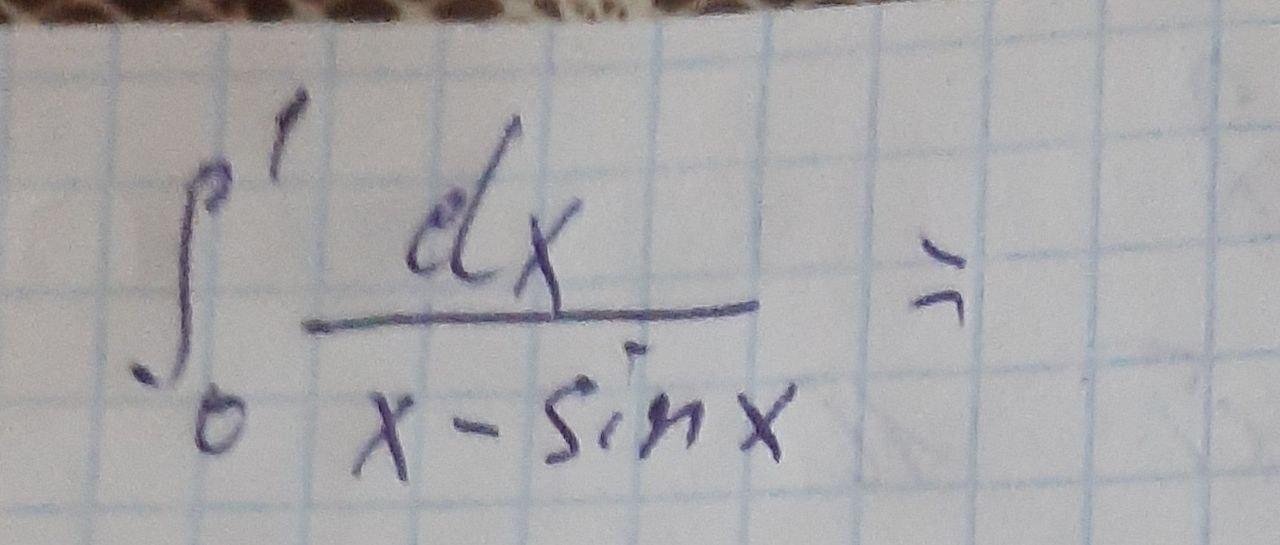
Ответы
Автор ответа:
0
Ответ:
Интеграл расходится
Пошаговое объяснение:
Исследуем на сходимость интеграл:
Следовательно данный интеграл расходится.
На отрезке от 0 до 1, sinx>0 ⇒ x-sinx < x, значит
Тогда по признаку сравнения из расходимости следует и расходимость
Похожие вопросы
Предмет: История,
автор: sofiya5175heg
Предмет: География,
автор: tieliehin
Предмет: Українська мова,
автор: sulimenkoanastasia6
Предмет: Геометрия,
автор: kasymovaa859
Предмет: Геометрия,
автор: fghgfhfghgfhrh