Предмет: Математика,
автор: manakhov8misha
Помогите решить очень необходим ответ
Приложения:
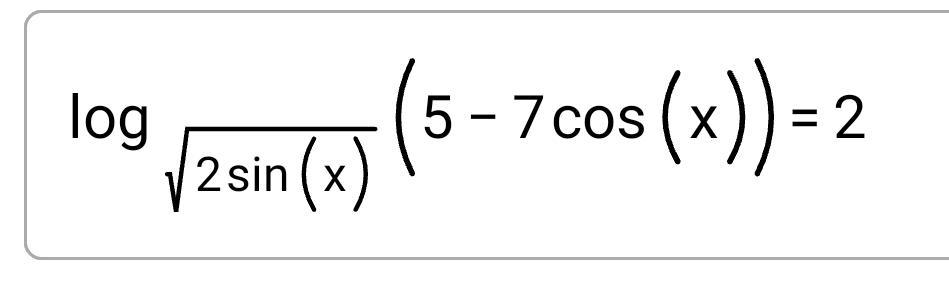

Ответы
Автор ответа:
1
Выпишем ОДЗ:
То есть,
Из непустой серии корней надо выкинуть те, которые не входят в ОДЗ:
1. Очевидно, что корни, удовлетворяющие , удовлетворяют условиям
и
из ОДЗ.
2. На единичной окружности корни, удовлетворяющие условию лежат на верхней части окружности. Таким образом, из серии корней
необходимо оставить только серию
.
Ответ.
P.S. Так же очевидно, что на промежуток попадёт только 1 корень.
Похожие вопросы
Предмет: Алгебра,
автор: Аноним
Предмет: Геометрия,
автор: snagorska57
Предмет: Алгебра,
автор: Аноним
Предмет: Биология,
автор: l6987106
Предмет: Математика,
автор: vghhhgy