Question

помогите решить логарифмическое уравнение log3(x+2)=2. через одз

Answer 1

Пошаговое объяснение:

решение задачи есть на фото

Answer 2

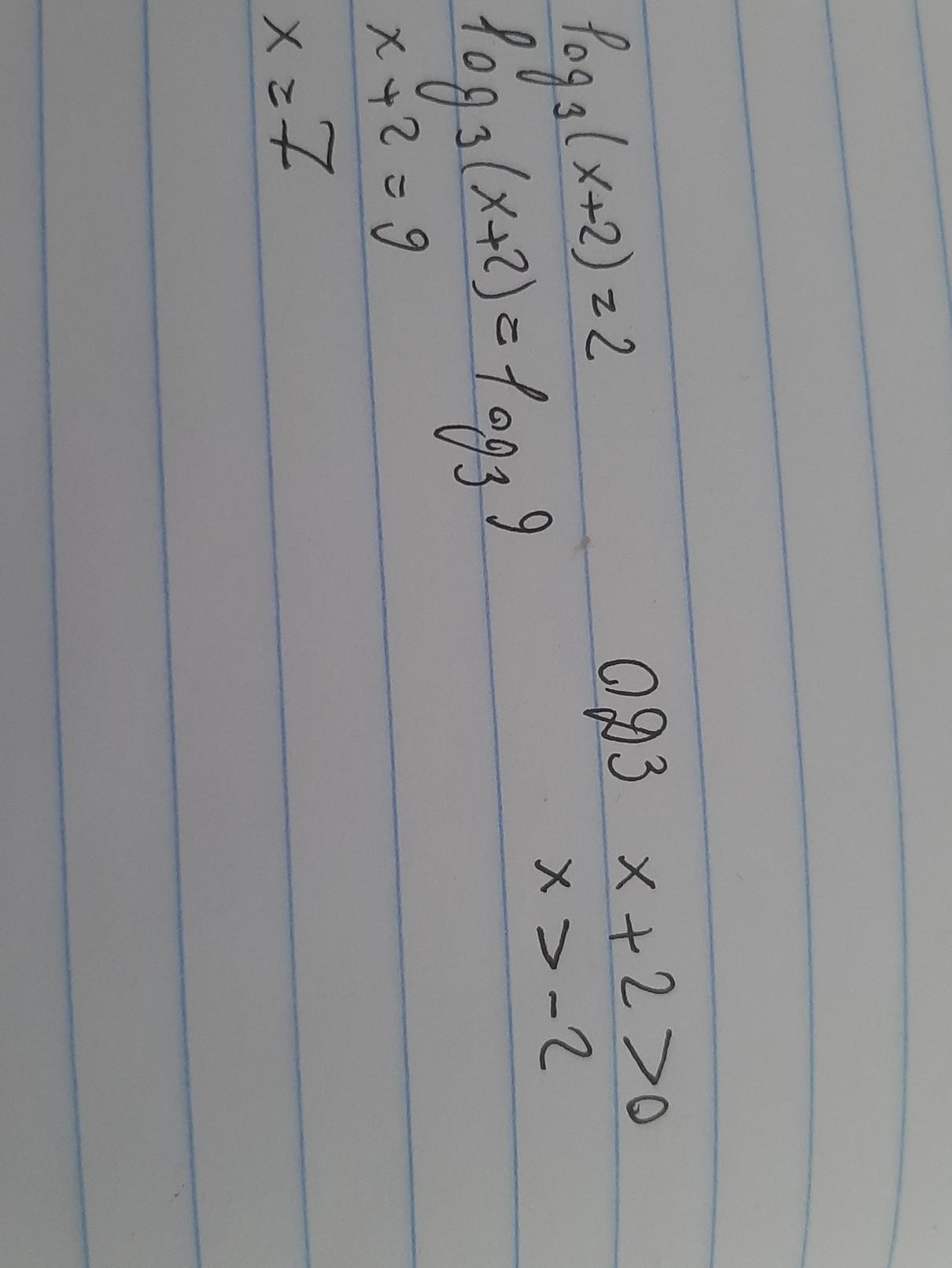
Ответ:

$x=7.$

Пошаговое объяснение:

Перед нами логарифмическое уравнение.

$log_{3} (x+2)=2;$              ОДЗ: $x+2 > 0;$

                                                $x > -2.$

При решении подобных уравнений нам нужно сделать так, чтобы с обеих частях уравнения были логарифмы с одинаковыми основаниями. В нашем случае, в левой части уравнения - логарифм по основанию 3, а с правой стороны - 2. Значит нам нужно превратить "двойку" в логарифм по основанию 3 какого-то числа.

Для этого просто вспомним, что логарифм - это степень, а основание логарифма - число, которое в степень возводят. Значит, чтобы найти число наше неизвестное число, возведём основание логарифма (то есть 3) во вторую степень (то есть в квадрат).

Получим:

$log_{3} 3^{2} = log_{3} 9.$

Значит:

$log_{3} (x+2)=log_{3} 9;$                                

Теперь, когда у нас в обеих частях уравнения логарифмы с одинаковыми основаниями, мы можем их сократить:

$x+2=9;$

$x=9-2;$

$x=7.$

__________
Удачи Вам! :)