Предмет: Математика,
автор: clownbut
Математика 10-11. Профиль. С подробным решением, пожалуйста.
Приложения:
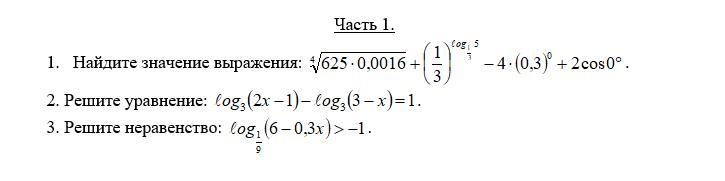
Ответы
Автор ответа:
1
Ответ:
1. 4; 2. 2; 3. х ∈ (-10; 20)
Пошаговое объяснение:
1. Найти значение выражения:
Воспользуемся свойством корня: корень из произведения равен произведению корней , основным логарифмическим тождеством и свойство степени: любое число в нулевой степени равно 1.
2.Решить уравнение :
Так как логарифм определен на множестве положительных чисел, то данное уравнение равносильно
Ответ: 2.
3. Решить неравенство:
Так как логарифм определен на множестве положительных чисел и функция монотонно убывает, то данное неравенство равносильно
Значит, х ∈ (-10; 20)
#SPJ1
Похожие вопросы
Предмет: Алгебра,
автор: VeronikaAva
Предмет: Українська мова,
автор: aliakohegarova
Предмет: Математика,
автор: foxy341092
Предмет: Геометрия,
автор: fghgfhfghgfhrh
Предмет: Астрономия,
автор: nmilcom