Предмет: Алгебра,
автор: artemdegterev05
помогите пожалуйста решить это
Приложения:
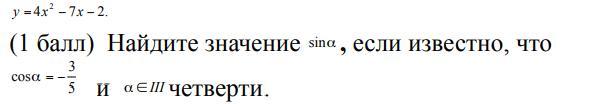
Ответы
Автор ответа:
1
Объяснение:
в ІІІ четверти sin(a)<0
Автор ответа:
0
α - угол третьей четверти , следовательно Sinα < 0 .
Похожие вопросы
Предмет: Геометрия,
автор: mellwizard
Предмет: Математика,
автор: aldabergenovanagima0
Предмет: Химия,
автор: nazardzhumaryk11
Предмет: Геометрия,
автор: Аноним
Предмет: Математика,
автор: JPobedinskiy