Предмет: Математика,
автор: Jeniksss
Прошу помогите пожалуйста срочно, нужен подробный ответ и с пояснением решения и с рисунком если он необходим в решении
Приложения:
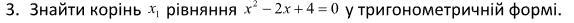
Ответы
Автор ответа:
2
Запись комплексного числа в тригонометрической форме :
z = r·(cosφ + isinφ)
Где
r - модуль комплексного числа
φ - аргумент комплексного числа
x² -2x + 4 = 0
D = 4 - 16 = -12
Похожие вопросы
Предмет: Українська література,
автор: id1619324
Предмет: Биология,
автор: Аноним
Предмет: Математика,
автор: sjifkrjx
Предмет: Физика,
автор: offtvchannel
Предмет: Русский язык,
автор: perch82