Помогите пожалуйста, с подробным решением

Ответы
Ответ: 4,5 кв.ед.
Объяснение:
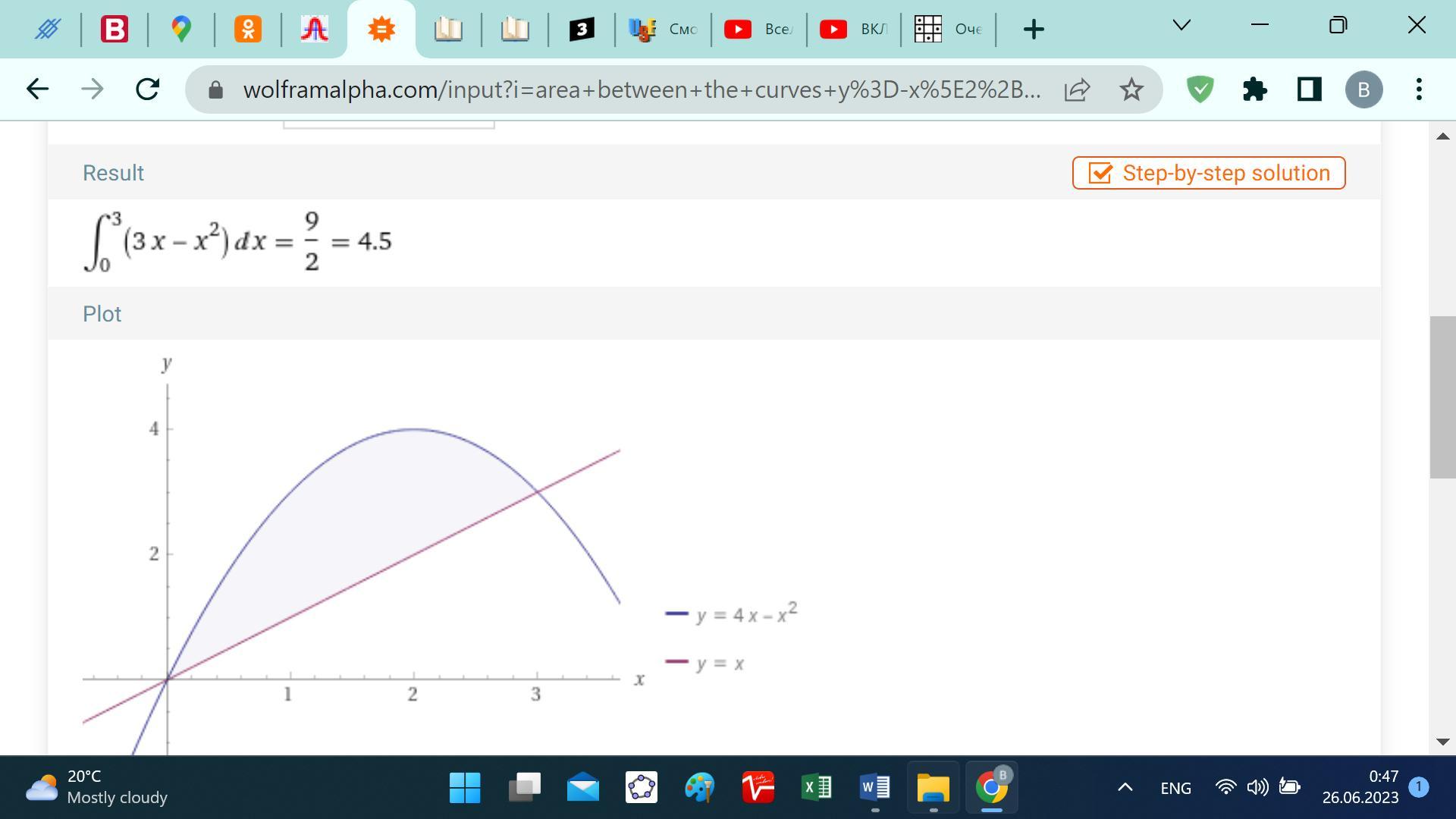
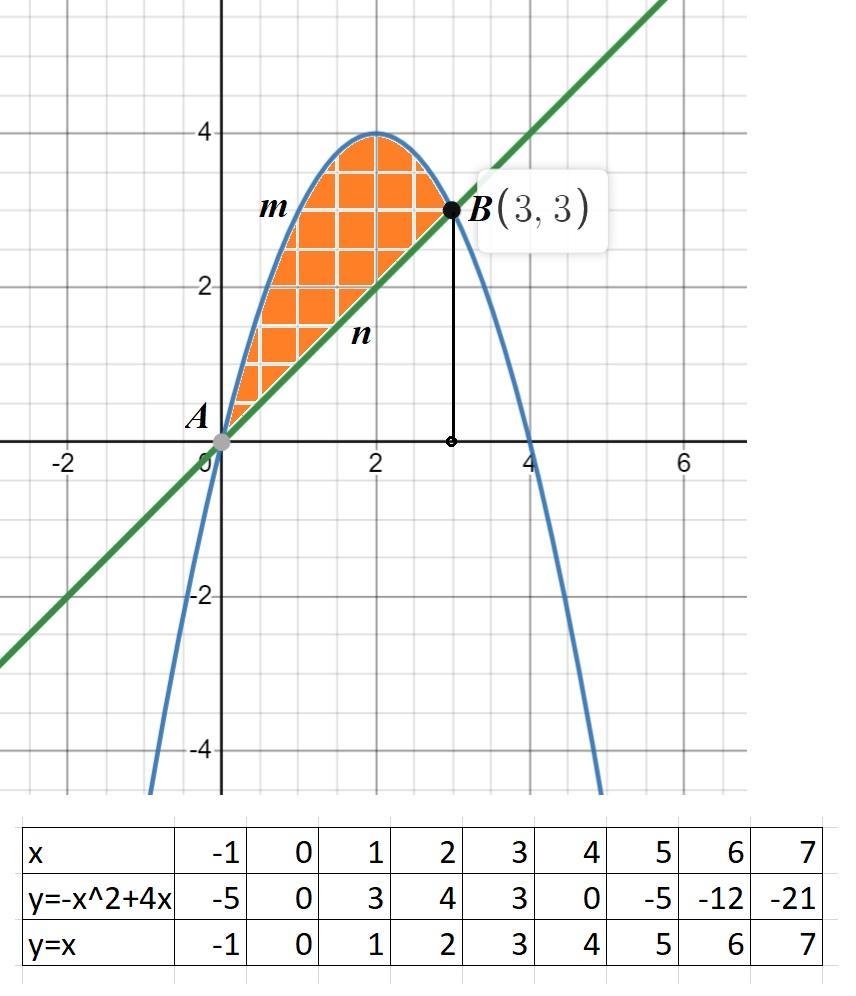
Строим графики функций y=-x^2+4x; y=x. (См. скриншот)
Площадь S(AmBn) = ∫ₐᵇf₁(x)dx - ∫ₐᵇf₂(x)dx.
Пределы интегрирования a=0; b=3.
f₁(x) = -x^2+4x;
f₂(x) = x.
f₁(x) > f₂(x). Тогда
S=∫₀³(-x^2+4x)dx - ∫₀³(x)dx = ∫₀³(-x^2+4x-x)dx = ∫₀³(-x^2)dx+3∫₀³(x)dx =
= -1/3(x³)|₀³ + 3/2(x²)|₀³ = -1/3(3³-0³) + 3/2(3²-0²) = -27/3+27/2 =
= -54/6 + 81/6 = (81-54)/6 = 27/6 = 9/2= 4,5 кв.ед.
Ответ: 4,5.
Объяснение:
Находим границы фигуры как точки пересечения графиков заданных функций.
Для этого приравняем функции.
-x² + 4x = x,
x² - 3x = 0,
x(x – 3) = 0.
Отсюда получаем 2 граничные точки: х = 0 и х = 3.
Площадь получаем как интеграл:
S = ʃ03(-x² + 4x – x)dx = ʃ03(-x² + 3x)dx =(-x³/3) + (3x²/2)|03 =
= (-27/3) +(3*9/2) – 0 = -9 + 13,5 = 4,5.