Предмет: Алгебра,
автор: jpjqycbhc7
Найти площадь $ фигуры, ограниченной параболами у-х^2 и у=2х^2-1.
Ответы
Автор ответа:
0
Ответ: 0.7695 кв.ед.
Объяснение:
Найти площадь S фигуры, ограниченной параболами
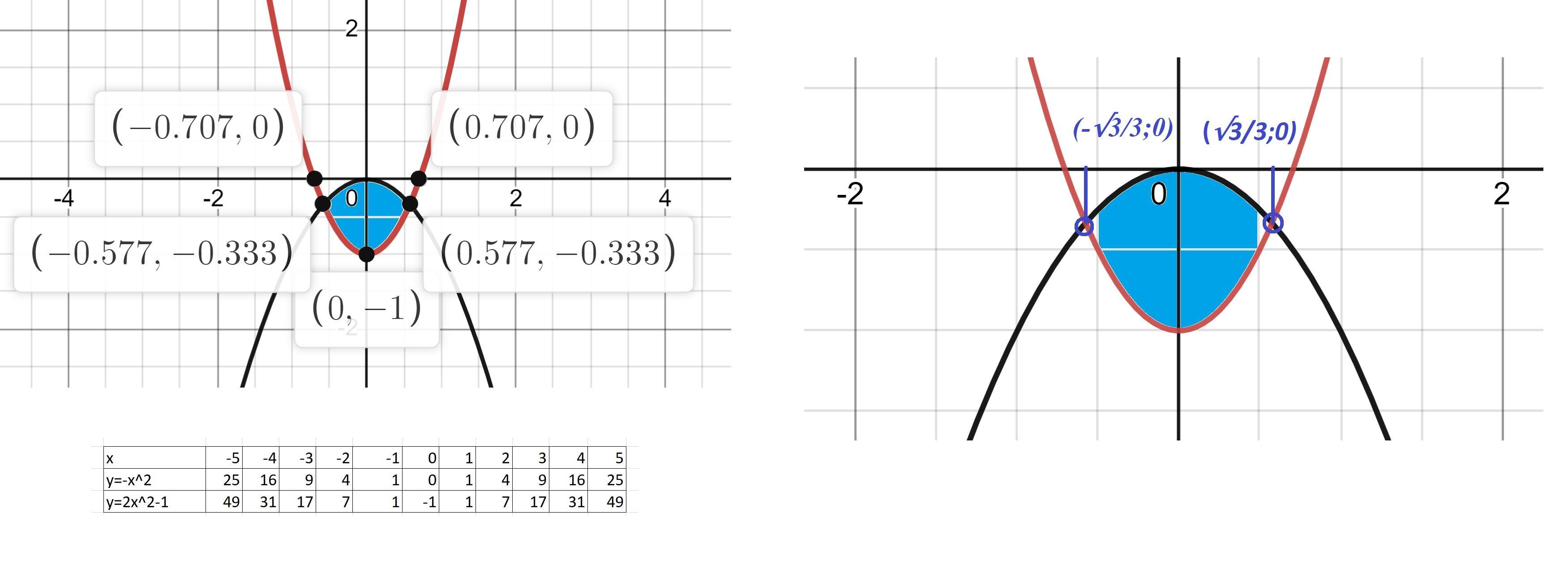
Строим графики функций у=-х^2; у=2х^2-1. (См. скриншот)
Площадь S=∫ₐᵇf₁(x)dx - ∫ₐᵇf₂(x)dx;
Находим пределы интегрирования. Приравняем правые чести функций:
-х^2 =2х^2-1;
3x^2 = 1;
x^2=1/3;
x=±1/√3 = ±√3/3 = ±0.577.
a=-0.577;
b=0.577.
Тогда
S=∫(от -0,577 до 0,577)((-х^2) - (2х^2-1))dx =
= ∫(от -0,577 до 0,577) (1-3x^2)dx =
= ∫(от -0,577 до 0,577) (1)dx -3 ∫(от -0,577 до 0,577)(x^2) =
= x|(от -0,577 до 0,577) - 3/3(x^3)|(от -0,577 до 0,577) =
= (0.577-(-0.577) - ((0.577)³ - (-0.577)³) = 1.154 - (0.1924 + 0.1921) =
= 1.154 - 0.3845 = 0.7695 кв.ед.
Приложения:
Похожие вопросы
Предмет: География,
автор: Аноним
Предмет: Химия,
автор: malyutenkovitalik
Предмет: Химия,
автор: mad7na
Предмет: Математика,
автор: d0r0tt
Предмет: Русский язык,
автор: neiliskz