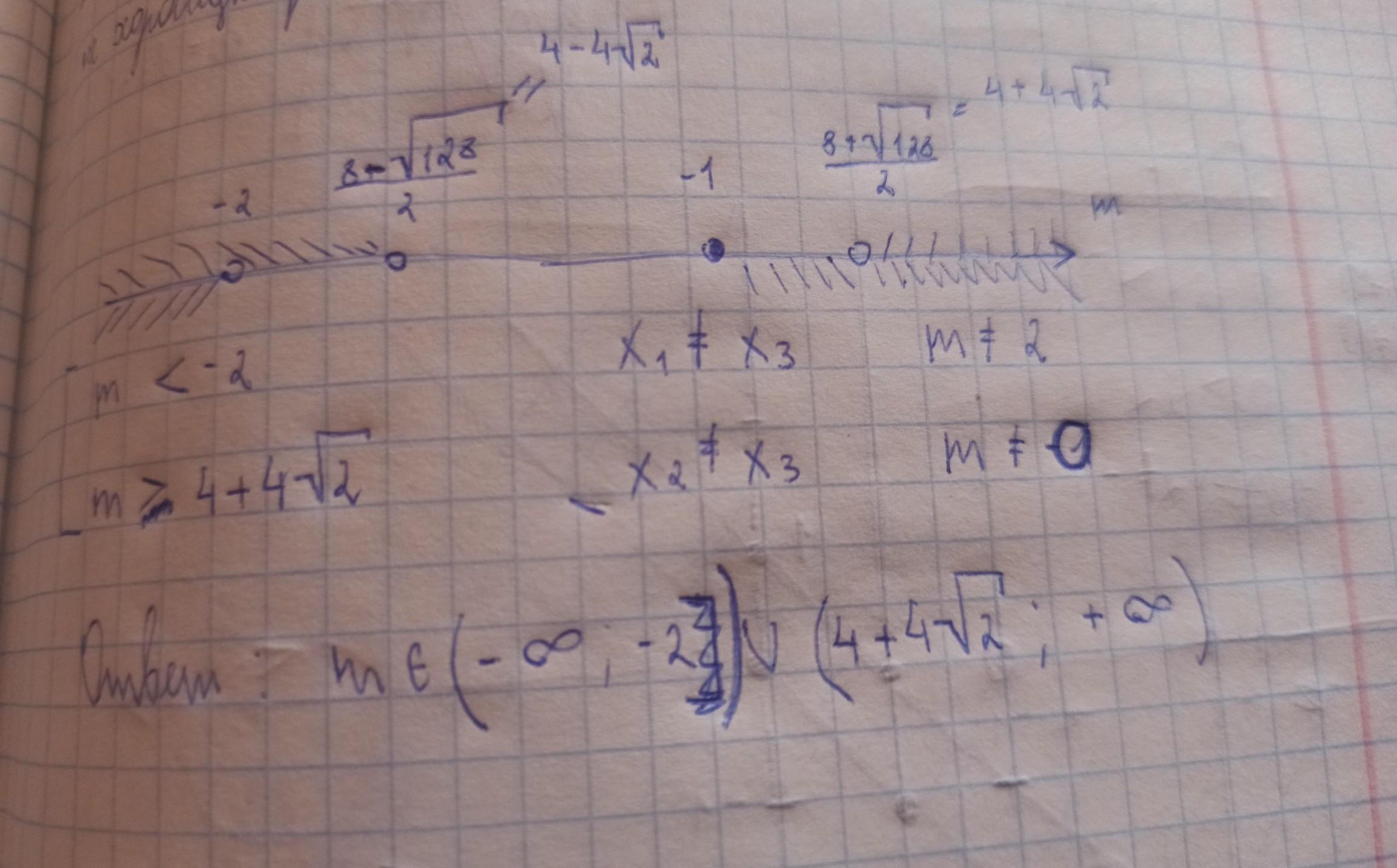Для яких значень дійсного параметра m многочлен f(x) = 2x^3 − (2 + m) x^2 + (2m + 2) x − m − 2 має три різні дійсні корені x1, x2, x3, які задовольняють умову (1/x1) + (1/x2) + (1/x3) >= 0?
Ответы
Ответ:
Знайдемо усі можливі значення параметра m, для яких многочлен f(x) має три різні дійсні корені x1, x2, x3.
За теоремою В'єта сума коренів многочлена з коефіцієнтами a, b, c, d дорівнює -b/a, тож сума коренів многочлена f(x) дорівнює (2 + m)/2.
Оскільки x1, x2, x3 є різними коренями многочлена f(x), то їх добуток x1x2x3 дорівнює -m/2.
Оскільки нас цікавить умова (1/x1) + (1/x2) + (1/x3) >= 0, то можемо розглядати два випадки:
1. Усі x1, x2, x3 мають один і той же знак. Тоді їх заміна на протилежні корені многочлена f(x) змінить умову на протилежну, тому можемо припустити, що всі x1, x2, x3 є додатні.
У такому випадку, оскільки x1x2x3 додатній, то всі три корені мають один і той же знак. Тоді sgn(x1) = sgn(x2) = sgn(x3) = +1 і (1/x1) + (1/x2) + (1/x3) >= 0, що еквівалентно x1x2 + x2x3 + x3x1 >= 0.
З теореми В'єта для многочлена f(x) маємо:
x1 + x2 + x3 = (2 + m)/2,
x1x2 + x2x3 + x3x1 = (2m + 2)/2,
x1x2x3 = -m/2.
Тоді sgn(x1) = sgn(x2) = sgn(x3) = +1 еквівалентно:
(x1 + x2 + x3)^2 >= 4x1x2 + 4x2x3 + 4x3x1,
або
(2 + m)^2 >= 8m + 16,
або
m^2 - 12m + 20 <= 0.
З цього нерівності маємо:
(m - 2)(m - 10) <= 0,
тобто -2 <= m <= 10.
2. Якщо серед трьох коренів f(x) є корені з різними знаками, то можна припустити, що x1 < 0 і x2, x3 > 0.
У такому випадку sgn(x1) = -1, sgn(x2) = sgn(x3) = +1, і умова (1/x1) + (1/x2) + (1/x3) >= 0 еквівалентна x2x3(x2 + x3) >= -x1, або (2m + 2)x2x3 >= -2m - 4 - (2 + m)x2x3 - 4x2x3x1.
З теореми В'єта маємо:
x1 + x2 + x3 = (2 + m)/2,
x1x2 + x2x3 + x3x1 = (2m + 2)/2,
x1x2x3 = -m/2.
Тоді x1 < 0 еквівалентно x1 + x2 + x3 < 0, тобто (2 + m)/2 < 0.
Також, оскільки x1 міститься у виразі для x1x2x3, то oскільки x1 < 0 і x2, x3 > 0, маємо x1x2x3 < 0, тобто m > 0.
Далі:
x2x3 = (2m + 2 - x1(x2 + x3))/2,
x1x2 + x2x3 + x3x1 = (2m + 2)/2.
Підставляючи ці вирази в нерівність (2m + 2)x2x3 >= -2m - 4 - (2 + m)x2x3 - 4x2x3x1, отримуємо:
(3 + m) x2x3 + 4x2x3x1 >= 4m + 4.
З 3 + m > 0 і 4x2x3x1 < 0 випливає:
(m - 5) x2x3 > 4m + 4,
тобто x2x3 < -(4m + 4)/(m - 5).
Оскільки x2x3 > 0, то маємо:
-(4m + 4)/(m - 5) < x2x3 < 0.
Записуючи це у вигляді проміжку, ми отримуємо:
-4 < m < 5.
Отже, об'єднуючи обидва випадки, ми отримуємо, що многочлен f(x) має три різні дійсні корені x1, x2, x3, що задовольняють умову (1/x1) + (1/x2) + (1/x3) >= 0, тоді і лише тоді, коли параметр m є проміжку:
-2 <= m <= 5.
Відповідь: -2 <= m <= 5.
Ответ:
m<-2 и m>4+4√2
Пошаговое объяснение:
Смотри на фото...
UPD: нашёл ошибку в моменте x1≠x3 и x2≠x3, исправляю:
x=1: 2-m+m+2=0
4=0, неверное тождество, таких m, что x1=1 или x2=1 нет