Предмет: Алгебра,
автор: jeng29
Помогите найти интеграл y=5-x², y=x+3
Ответы
Автор ответа:
0
Решение снизу:
............
Приложения:
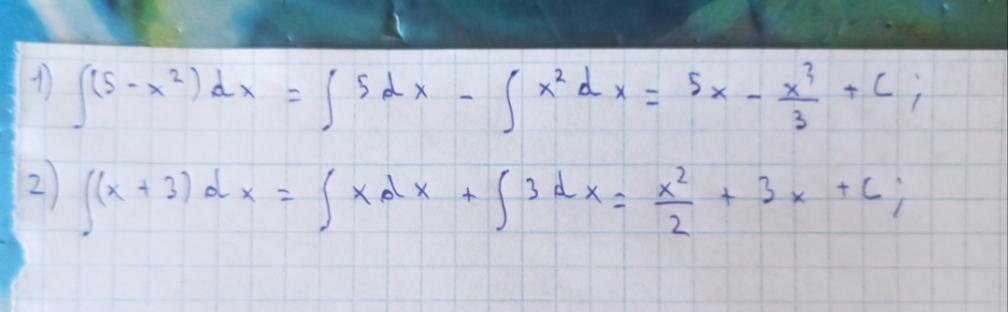
Автор ответа:
0
Чтобы найти интеграл функции, вам нужно найти площадь между графиками этих двух функций.
Для начала, найдем точки пересечения этих двух функций, приравняв их:
5 - x² = x + 3
Приведем уравнение к квадратичному виду:
x² + x - 2 = 0
Решим это квадратное уравнение:
(x + 2)(x - 1) = 0
Таким образом, получаем две точки пересечения: x = -2 и x = 1.
Теперь мы можем найти интеграл функции, разбив его на две части:
∫[a,b] (f(x) - g(x)) dx
где a и b - точки пересечения функций, f(x) - верхняя функция, g(x) - нижняя функция.
Для нашего случая, верхняя функция f(x) = 5 - x², а нижняя функция g(x) = x + 3.
Таким образом, интеграл будет:
∫[-2,1] (5 - x² - (x + 3)) dx
Выполним расчет:
∫[-2,1] (2 - x - x²) dx
Интегрируя каждый член по отдельности, получаем:
∫[-2,1] (2 dx) - ∫[-2,1] (x dx) - ∫[-2,1] (x² dx)
Интегрируя, получаем:
[2x] от -2 до 1 - [x²/2] от -2 до 1 - [x³/3] от -2 до 1
Вычисляем значения в пределах интегрирования:
[2(1) - 2(-2)] - [(1²/2) - (-2²/2)] - [(1³/3) - (-2³/3)]
= [2 + 4] - [1/2 - 4/2] - [1/3 + 8/3]
= 6 - [-3/2] - 9/3
= 6 + 3/2 - 3
= 12/2 + 3/2 - 6/2
= 15/2 - 6/2
= 9/2
Таким образом, интеграл функции y = 5 - x², ограниченный функцией y = x + 3, равен 9/2 или 4.5.
Для начала, найдем точки пересечения этих двух функций, приравняв их:
5 - x² = x + 3
Приведем уравнение к квадратичному виду:
x² + x - 2 = 0
Решим это квадратное уравнение:
(x + 2)(x - 1) = 0
Таким образом, получаем две точки пересечения: x = -2 и x = 1.
Теперь мы можем найти интеграл функции, разбив его на две части:
∫[a,b] (f(x) - g(x)) dx
где a и b - точки пересечения функций, f(x) - верхняя функция, g(x) - нижняя функция.
Для нашего случая, верхняя функция f(x) = 5 - x², а нижняя функция g(x) = x + 3.
Таким образом, интеграл будет:
∫[-2,1] (5 - x² - (x + 3)) dx
Выполним расчет:
∫[-2,1] (2 - x - x²) dx
Интегрируя каждый член по отдельности, получаем:
∫[-2,1] (2 dx) - ∫[-2,1] (x dx) - ∫[-2,1] (x² dx)
Интегрируя, получаем:
[2x] от -2 до 1 - [x²/2] от -2 до 1 - [x³/3] от -2 до 1
Вычисляем значения в пределах интегрирования:
[2(1) - 2(-2)] - [(1²/2) - (-2²/2)] - [(1³/3) - (-2³/3)]
= [2 + 4] - [1/2 - 4/2] - [1/3 + 8/3]
= 6 - [-3/2] - 9/3
= 6 + 3/2 - 3
= 12/2 + 3/2 - 6/2
= 15/2 - 6/2
= 9/2
Таким образом, интеграл функции y = 5 - x², ограниченный функцией y = x + 3, равен 9/2 или 4.5.
Похожие вопросы
Предмет: Физика,
автор: Аноним
Предмет: Математика,
автор: YianXixi
Предмет: Математика,
автор: tanakolesnik531
Предмет: История,
автор: Sviridov228
Предмет: Математика,
автор: traptogan