Предмет: Математика,
автор: kameyaxx
помогите с геометрией 7 класс
решите номер 4 и 5
Приложения:
Ответы
Автор ответа:
0
Пошаговое объяснение:
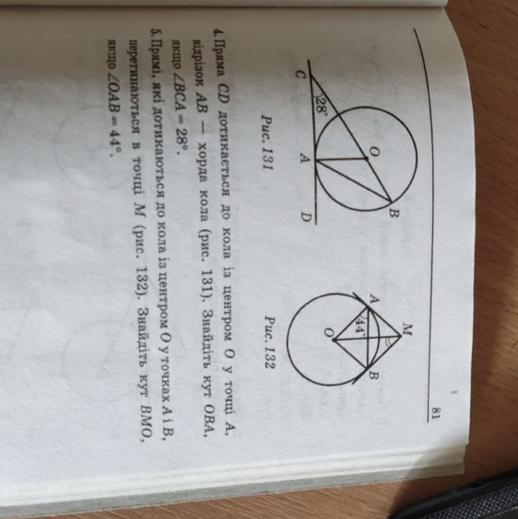
4.
касательная к окружности перпендикулярна радиусу проведённому в точку касания, значит ∠САО=90°
∠СОА=90-28=62°
∠АОВ=180-∠СОА=180-62=118° - как смежные
∆АОВ - равнобедреный,ОА=ОВ - как радиусы
∠ОВА=∠ОАВ=(180-∠АОВ):2=
=(180-118):2=31°
ответ: 31°
5.
∆АОВ - равнобедреный: АО=ОВ - как радиусы.
∠ОВА=∠ОАВ=44°.
касательная к окружности перпендикулярна радиусу проведённому в точку касания, значит∠ОВМ=90°.
∠МВА=90-∠ОВА=90-44=46°
по свойству касательных проведенных из одной точки
МА=МВ, значит ∆АМВ - равнобедреный
∠АМВ=180-2•МВА=180-2•46=88°
МО в равнобдренном треугольнике является высотой ,биссектриса и медианой , тогда
∠ВМО=∠АМВ:2=88:2=44°
ответ: 44°
Похожие вопросы
Предмет: Другие предметы,
автор: marina801polishchyk
Предмет: Українська література,
автор: eseniya199018
Предмет: Музыка,
автор: vmvova4
Предмет: Физика,
автор: SROCHNO21321