Предмет: Алгебра,
автор: dddus
Решите уравнение которое на фото
Приложения:
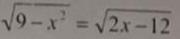
Ответы
Автор ответа:
1
Возведём обе стороны уравнения в квадрат и решим:
Выполним проверку:
Получили отрицательный корень, такого быть не может, значит
Аналогичная ситуация будет со вторым корнем уравнения. При проверке получим отрицательный корень, такого быть не может, значит
Следовательно уравнение не имеет действительных решений
Похожие вопросы
Предмет: Литература,
автор: sashka26032010
Предмет: Математика,
автор: irinaleonidova179
Предмет: Литература,
автор: yana5460
Предмет: Математика,
автор: Alxazovakemale
Предмет: Немецкий язык,
автор: AylinIskakova99