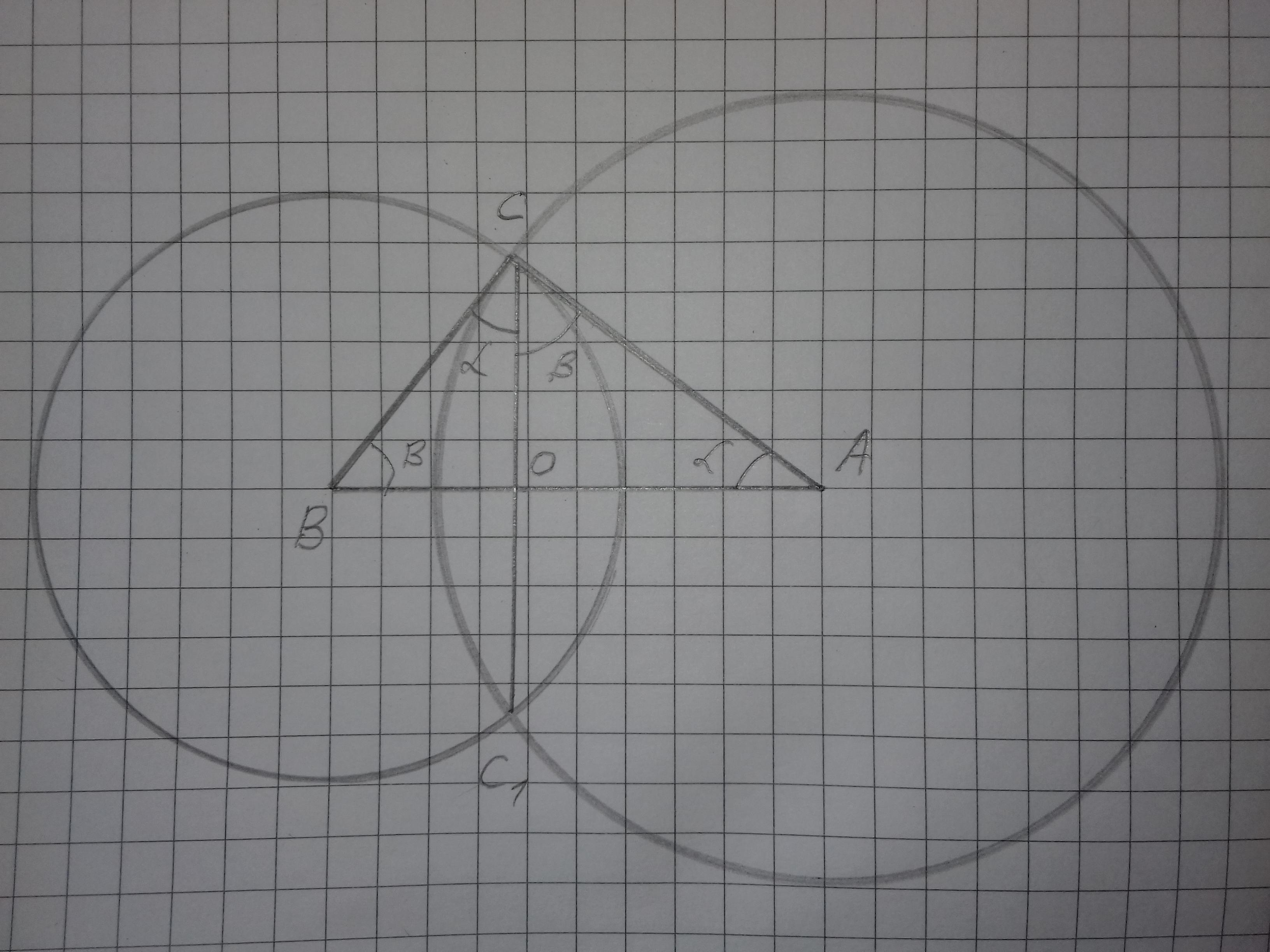Радиусы шаров равны 4 см и 3 см, а расстояние между их центрами 5 см. Найдите длину линии, по которой пересекаются их поверхности.
Ответы
Відповідь:
Длина линии, по которой пересекаются поверхности двух шаров равна 15,1 см.
Покрокове пояснення:
Поскольку сумма радиусов двух шаров ( 4 + 3 = 7 см ) больше, чем расстояние между их центрами ( 5 см ), то шары пересекаются по окружности.
Построим сечение, проходящее через центры шаров. Первый шар с центром в точке А с радиусом R1 = АС = 4 см, второй шар с центром в точке В с радиусом R2 = ВС = 3 см. Расстояние между центрами шаров АВ = 5 см. Шары пересекаются по окружности СС1 ( СС1 - это диаметр окружности пересечения двух шаров ).
Треугольник АВС - прямоугольный с прямым углом С = 90°. Это можно проверить по теореме Пифагора:
АВ² = АС² + ВС²
5² = 4² + 3²
25 = 16 + 9
25 = 25
Пересечение отрезков АВ и СС1 - точка О, а отрезок СО - высота треугольника АВС.
Рассмотрим треугольники АВС, АСО и СВО - они подобные ( все три соответствующие углы треугольников равны ).
∆АВС
∠АСВ = 90°
∠САВ = α
∠СВА = β
∆АСО
∠АОС = 90°
∠ОАС = α
∠ОСА = β
∆СВО
∠СОВ = 90°
∠ОСВ = α
∠ОВС = β
∆АВС ~ ∆АСО ~ ∆СВО
АВ ( ∆АВС ) ~ АС ( ∆АСО ) ~ СВ ( ∆АСО ) ( как гипотенуза соответствующих треугольников ).
АС ( ∆АВС ) ~ АО ( ∆АСО ) ~ СО ( ∆АСО ) ( как катет прилежащий к ∠α соответствующих треугольников ).
ВС ( ∆АВС ) ~ СО ( ∆АСО ) ~ ВО ( ∆АСО ) ( как катет прилежащий к ∠β соответствующих треугольников ).
Коэффициент подобия треугольников АВС и АСО:
k1 = АС / АВ = 4/5
или АС = k1 × АВ = 4/5 × АВ
Получаем:
АС = 4/5 × АВ = 4/5 × 5 = 20/5 = 4 см.
АО = 4/5 × АС = 4/5 × 4 = 16/5 = 3,2 см.
СО = 4/5 × ВС = 4/5 × 3 = 12/5 = 2,4 см.
Коэффициент подобия треугольников АВС и СВО:
k2 = СВ / АВ = 3/5
или СВ = k1 × АВ = 3/5 × АВ
Получаем:
СВ = 3/5 × АВ = 3/5 × 5 = 15/5 = 3 см.
СО = 3/5 × АС = 3/5 × 4 = 12/5 = 2,4 см.
ВО = 3/5 × ВС = 3/5 × 3 = 9/5 = 1,8 см.
Мы получили одинаковую величину СО ( радиус окружности пересечения двух шаров ) рассчитанную по двум треугольникам.
Также сумма АО и ВО равна АВ:
АВ = АО + ВО
5 = 3,2 + 1,8
5 = 5
Для проверки правильности расчетов проверим выполняется ли теорема Пифагора для ∆АСО и ∆СВО ( так как они оба прямоугольные ):
для ∆АСО
АС² = АО² + СО²
4² = 3,2² + 2,4²
16 = 10,24 + 5,76
16 = 16
для ∆СВО
СВ² = СО² + ВО²
3² = 2,4² + 1,8²
9 = 5,76 + 3,24
9 = 9
Все правильно.
Мы нашли радиус окружности пересечения двух шаров R = СО = 2,4 см.
Найдем длину линии, по которой пересекаются поверхности двух шаров.
Поскольку два шара пересекаются по окружности, то нам необходимо найти длину окружности:
L = 2 × π × R = 2 × π × 2,4 = 4,8 × π = 15,1 см.