Предмет: Математика,
автор: nastabbabcuk
log7(-x) + log7(1-x) = log7 (x + 3)
Ответы
Автор ответа:
1
ОДЗ:
Воспользуемся свойством логарифмов :
Основания логарифмов справа и слева равны, значит можно их опустить:
x = 3 не входит в ОДЗ, значит уравнение имеет одно решение x = -1
Ответ: x = -1
experced:
откройте с компьютера
Автор ответа:
1
Відповідь: -1
Покрокове пояснення:
Приложения:
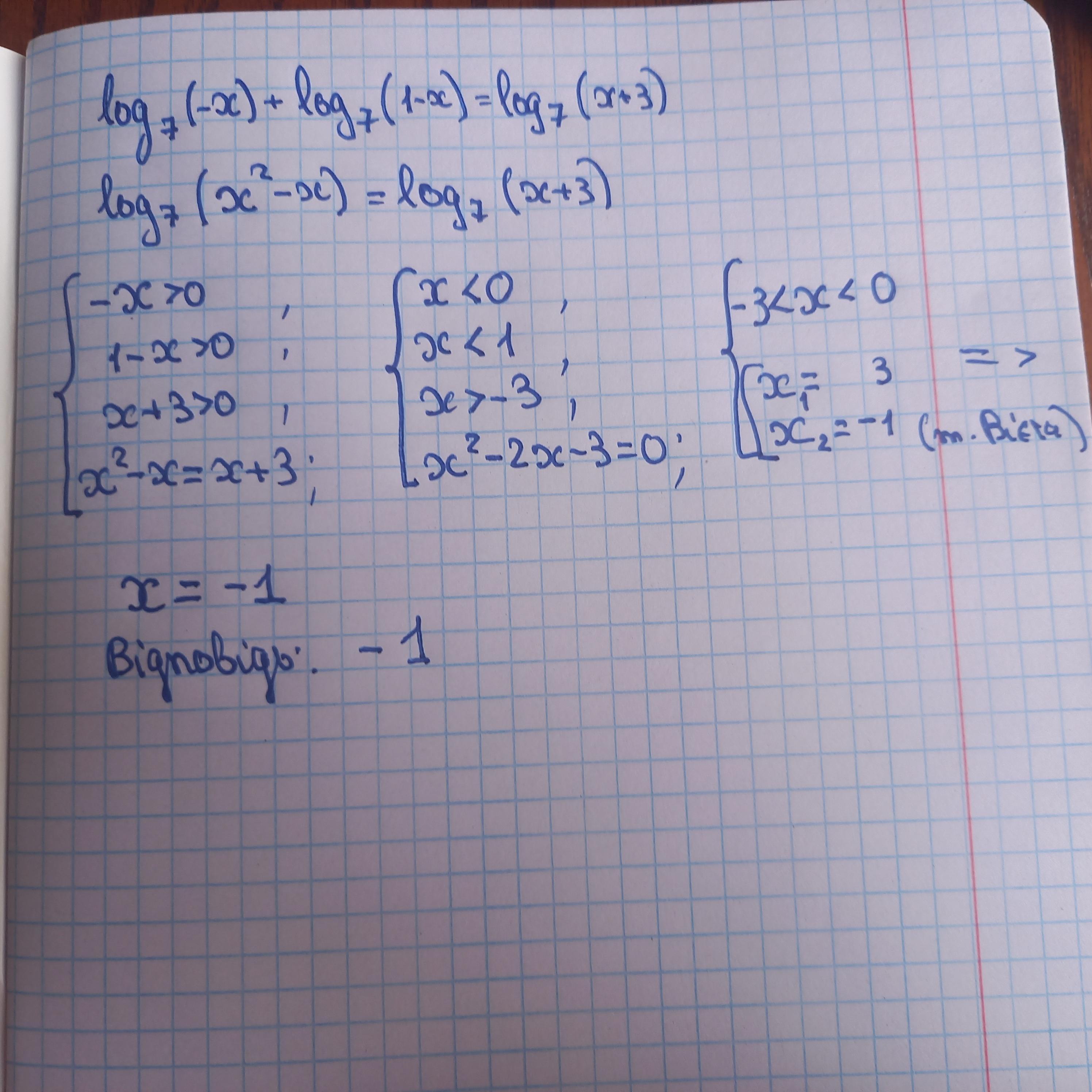
Похожие вопросы
Предмет: Математика,
автор: ff058
Предмет: Математика,
автор: babuskamama61
Предмет: География,
автор: danabahnak
Предмет: Химия,
автор: satybaldinova10
Предмет: Химия,
автор: platonovpixar