Скласти блок-схеми розв’язку задач лінійних та розгалужених алгоритмів.
Лінійні алгоритми
a) Скласти блок-схему алгоритму знаходження одного значення функції
b) Скласти блок-схему алгоритму знаходження одного значення поліному,
попередньо привівши його до формули Горнера.
Оба задания в скриншоте. Будь ласка, ще звіт по цим завданням.
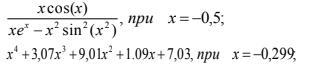
Ответы
Блок-схемы для кода прикрепил.
Более подробный алгоритм:
1. e^(2*x) + 0.5e^(3*x) + 0.5e^x
1) cos(x) = cos(-0.5)
2) e^x = e^(-0.5)
3) sin(x^2) = sin((-0.5)^2)
4) x * cos(x) = -0.5 * cos(-0.5)
5) x * e^x = -0.5 * e^(-0.5)
6) x^2 * sin(x^2)^2 = (-0.5)^2 * sin((-0.5)^2)^2
7) x * cos(x) / (x * e^x - x^2 * sin(x^2)^2) = (-0.5 * cos(-0.5)) / (-0.5 * e^(-0.5) - (-0.5)^2 * sin((-0.5)^2)^2)
8) Вывод результата.
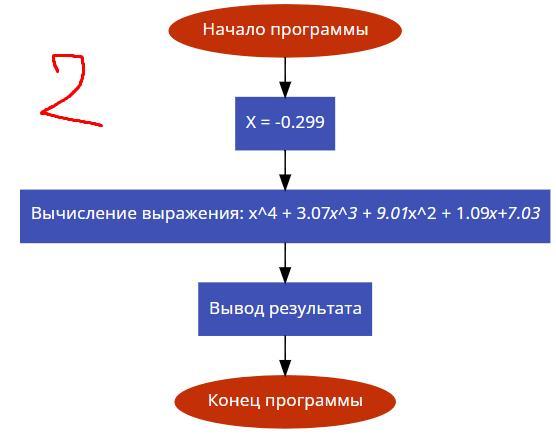
2. x^4 + 3.07*x^3 + 9.01*x^2 + 1.09*x+7.03 = y = (((x + 3.07)*x + 9.01)*x + 1.09)*x + 7.03 - по формуле Горнера.
1) x = -0.299
2) y = 7.03
3) y = y + 1.09 * x
4) y = y + 9.01 * x^2
5) y = y + (x + 3.07) * x^2
6) y = y + ((x + 3.07) * x + 9.01) * x
7) y = y + (((x + 3.07) * x + 9.01) * x + 1.09) * x
8) y = y + ((((x + 3.07) * x + 9.01) * x + 1.09) * x + 7.03)
Вывод результата.
Код на Python задача 1:
import math
x = -0.5
y = (x * math.cos(x)) / (x * math.exp(x) - x**2 * math.sin(x**2)**2)
print("Значение y при x = -0.5:", y)
Результат: : 1.3773886780499567.
Код на Python задача 2:
x = -0.299
y = x**4 + 3.07*x**3 + 9.01*x**2 + 1.09*x + 7.03
print("Значение y при x = -0.299:", y)
Результат: 7.43552168887.