Предмет: Алгебра,
автор: eoeiieod
ПОМОГИТЕ СРОЧНО
№1 найти sin a
№2 найти sin2a
Приложения:
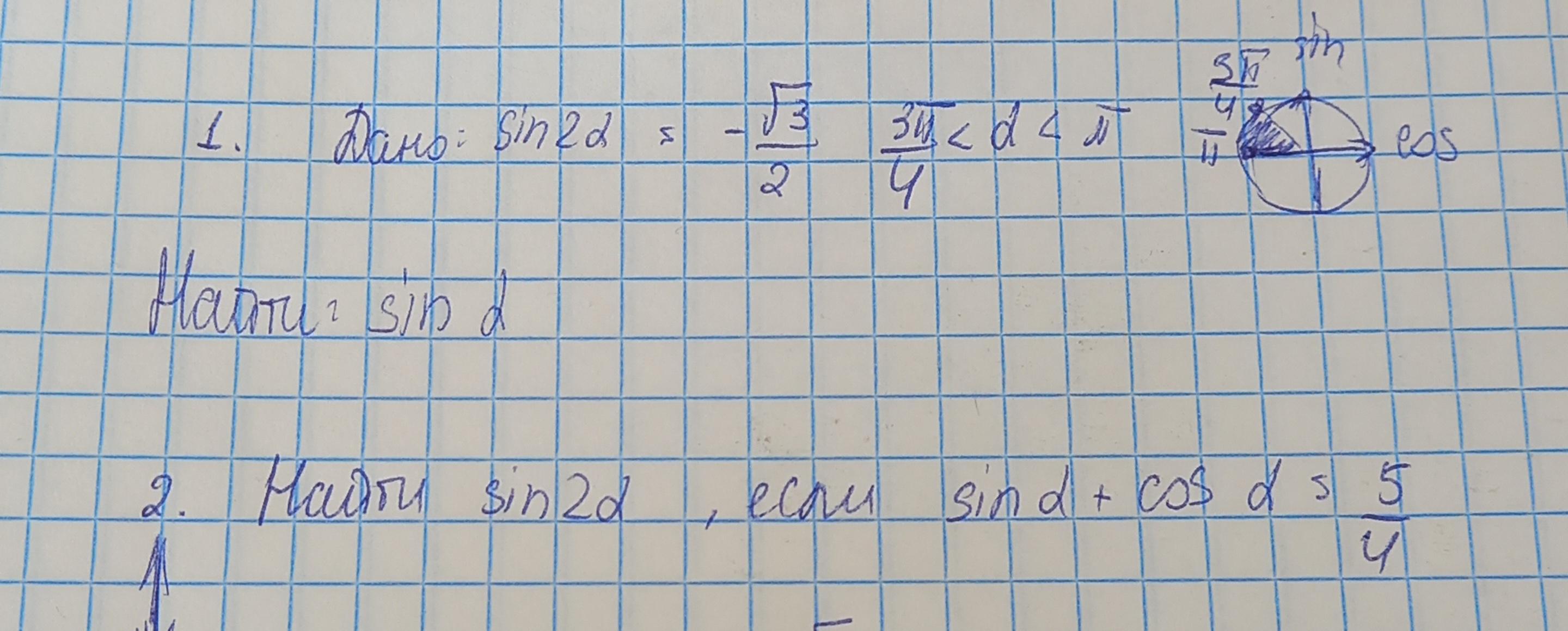
Ответы
Автор ответа:
0
Объяснение:
1.
Пусть sin²α=t ⇒
Ответ: sinα=1/2, sinα=√3/2.
2.
Ответ: sin2α=9/16.
Похожие вопросы
Предмет: Українська мова,
автор: udar43konst
Предмет: Химия,
автор: litvinurij417
Предмет: Геометрия,
автор: aleksandrabezverha84
Предмет: Биология,
автор: pahomenkodaniil93
Предмет: Обществознание,
автор: mariaismailova923