Предмет: Математика,
автор: vini4enkojarik72
Математика логарифмы помогите кто шарит пожалуйста
Приложения:
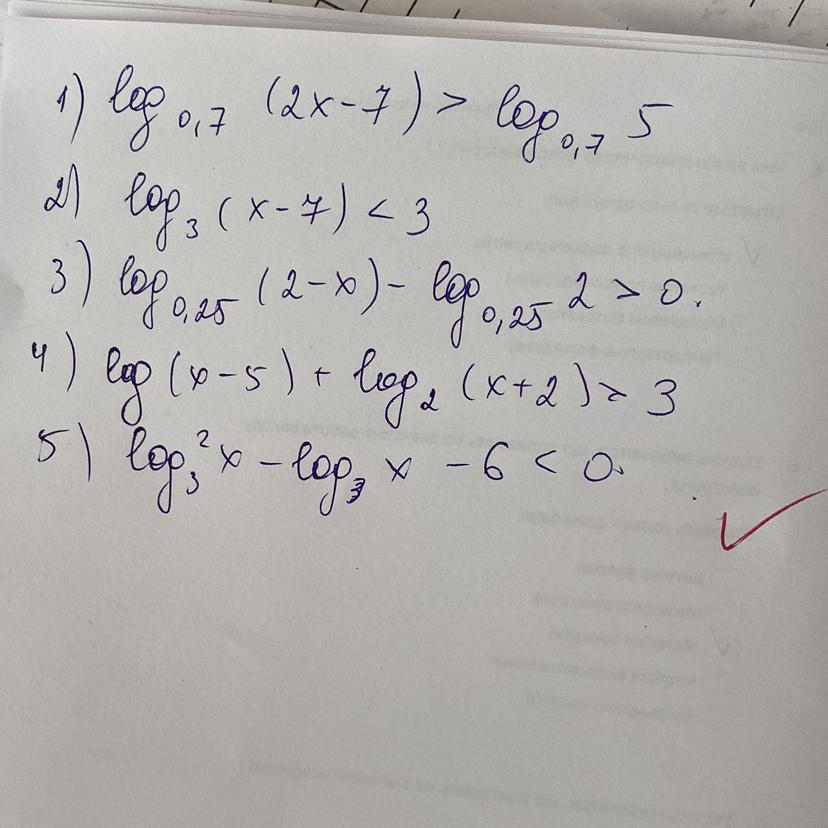
Ответы
Автор ответа:
1
Ответ:
Основание логарифма 0 < 0,7 < 1 , поэтому функция убывающая и
Основание логарифма 3 > 1 , поэтому функция возрастающая и
.
Замена:
Приложения:


vini4enkojarik72:
а что с пятым?
c ним всё в порядке
В пятом 1/9 и 27
Автор ответа:
1
1)
ОДЗ:
Убывающая функция, знак меняем
2)
ОДЗ:
Возрастающая функция, знак не меняем
3)
ОДЗ:
Убывающая функция, знак меняем
4)
ОДЗ:
Возрастающая функция, знак не меняем
5)
ОДЗ:
Возрастающая функция, знак не меняем
Похожие вопросы
Предмет: Физика,
автор: agolovchenko2701
Предмет: Физика,
автор: suyyoad
Предмет: Українська мова,
автор: arina608060
Предмет: Физика,
автор: Vadimkostyuchenko196
Предмет: Русский язык,
автор: Andreychikyc