Предмет: Алгебра,
автор: osheraliev
Вычислить, при sina=⅙
Cos(π/2+a)+cos(3π/2-a)
Приложения:
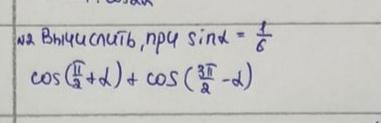
Ответы
Автор ответа:
1
Відповідь:
Пояснення:
osheraliev:
Спасибо
Автор ответа:
2
Так как у нас pi/2 и 3pi/2 , то косинус меняется на синус. В первом случае это 2 четверть, а во втором 3 четверть, поэтому синус отрицательный
Спасибо
Похожие вопросы
Предмет: Математика,
автор: Sofixp
Предмет: Химия,
автор: kriukolexiy08
Предмет: Химия,
автор: jokhdfrffd81
Предмет: Математика,
автор: m2002step
Предмет: Геометрия,
автор: kiril13082004