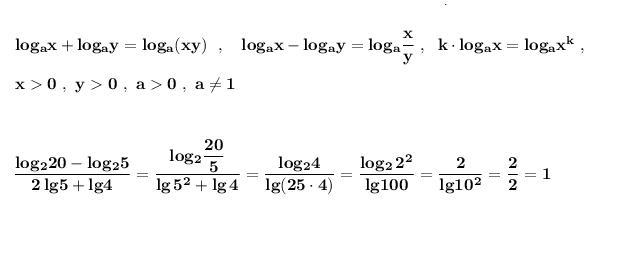Question

Обчислити:
log2^20-log2^5/2lg5+lg4 =

Answer 1

Ответ:

Давайте розкриємо вираз та застосуємо правила логарифмів:

log2^20 - log2^5/2 + lg5 + lg4

За правилом логарифмів log(a) - log(b) = log(a/b), можемо скористатися ним для першого та другого доданків:

log2^20 - log2^5/2 + lg5 + lg4 = log2^(20 - 5/2) + lg5 + lg4

Далі, за правилом логарифму log(a) + log(b) = log(a * b), можемо об'єднати третій та четвертий доданки:

log2^(20 - 5/2) + lg5 + lg4 = log2^(20 - 5/2) + lg(5 * 4)

Знаходимо значення виразу 20 - 5/2:

20 - 5/2 = 20 - 2.5 = 17.5

Підставляємо отримане значення назад:

log2^(20 - 5/2) + lg(5 * 4) = log2^17.5 + lg(20)

Значення log2^17.5 та lg(20) можна обчислити числово за допомогою калькулятора або математичного програмного забезпечення.

Пошаговое объяснение:

Answer 2

Ответ:

Вычислить значение . Применяем свойства логарифмов :

$\bf log_{a}x+log_{a}y=log_{a}(xy)\ \ ,\ \ \ log_{a}x-log_{a}y=log_{a}\dfrac{x}{y}\ ,\ \ k\cdot log_{a}x=log_{a}x^{k}\ ,\\\\x > 0\ ,\ y > 0\ ,\ a > 0\ ,\ a\ne 1$

$\bf \dfrac{log_220-log_25}{2\, lg5+lg4}=\dfrac{log_2\dfrac{20}{5}}{lg\, 5^2+lg\, 4}=\dfrac{log_24}{lg(25\cdot 4)}=\dfrac{log_2\, 2^2}{lg100}=\dfrac{2}{lg10^2}=\dfrac{2}{2}=1$