Предмет: Геометрия,
автор: zmeura1204
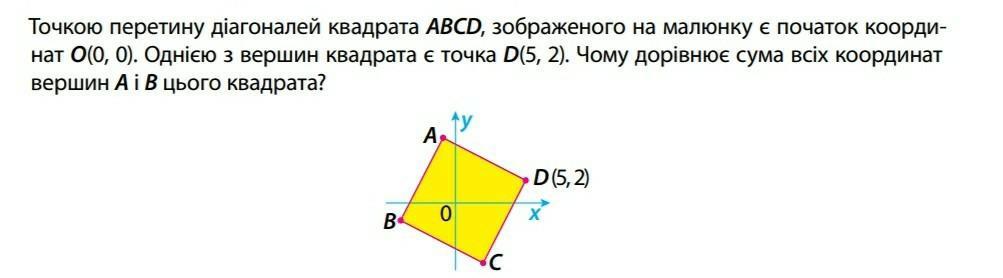
Точкой пересечения диагоналей квадрата ABCD, изображённого на рисунке является начало координат O(0, 0). Одной из вершин квадрата является точка D(5, 2). Чему равна сумма всех координат вершин А и В этого квадрата?
Приложения:
Ответы
Автор ответа:
1
Ответ: =10
Объяснение:
Согласно условия координаты вектора ОА=(5;2)
Поскольку в квадрате диагонали перпендикулярны, то
вектора ОА и ОВ перпендикулярны. Более того - поскольку точка пересечения диагоналей О делит их пополам , то ОА=ОВ
=> OA=OB=√29
Поскольку вектора ОА и ОВ перпендикулярны, то
их скалярное произведение равно 0
Xa*Xb+Ya*Yb=0 => 5*Xb-2*Yb=0 => 5Xb=2*Yb => Yb=5*Xb/2=2.5*Xb
также ОВ=ОА=√29 => Xb²+Yb²=29 => Xb² +6.25Xb²=29
7.25*Xb²=29
Xb²=4 => Xb1=-2 м Xb2=2
По рисунку точка В находится во втором квадранте
=> Xb<0 => Xb=-2 => Yb=5
=> Xb+Xa+Yb+Ya=5+5+2-2=10
Похожие вопросы
Предмет: Английский язык,
автор: ekkartviktoria89
Предмет: Экономика,
автор: triplesixgodz
Предмет: Обществознание,
автор: samira123ggcbklara
Предмет: Алгебра,
автор: vanserebro
Предмет: Математика,
автор: Kokokosh