Предмет: Алгебра,
автор: vaclav22
Найти частное решение дифференциального уравнения
Приложения:
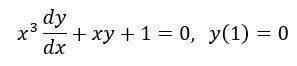
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Поскольку достаточно того, чтобы функция существовала в точке x = 1, разделим обе части на x³:
Представим функцию в виде произведения двух функций (метод Бернулли): . Тогда
Подберём функцию v так, чтобы :
Подставив в дифференциальное уравнение, получаем:
Возьмём интеграл правой части:
Таким образом,
Найдём C путём подстановки x = 1 и y = 0:
Таким образом, частное решение:
Похожие вопросы