Предмет: Математика,
автор: sergiodarker1
u = sqrt(z) * sin(y/x) ;du| M 0 (2:0:4) =
Ответы
Автор ответа:
1
Ответ:
Найти дифференциал функции в точке М₀ .
Формула : .
Приложения:
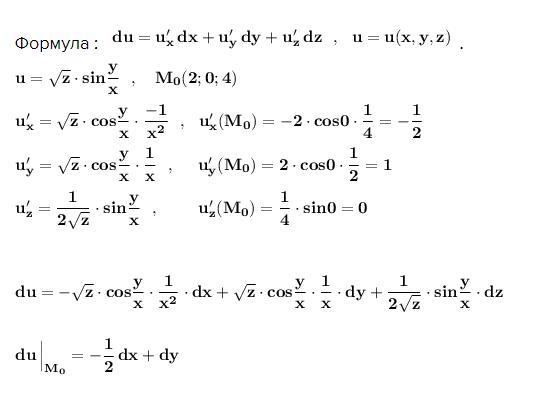
sergiodarker1:
Спасибо вам большое
Похожие вопросы
Предмет: Литература,
автор: koniahavasyl
Предмет: Английский язык,
автор: nazalalatan
Предмет: Литература,
автор: p0975732815
Предмет: Математика,
автор: pm81
Предмет: Геометрия,
автор: tornado19234p3zt0x