Предмет: Математика,
автор: denversvoboda
ЗНАЙТИ ПОХІДНУ ФУНКЦІЇ В ТОЧЦІІ НА ФОТО
Приложения:
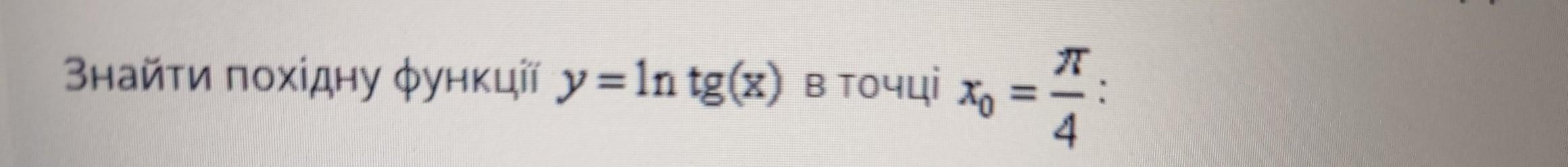
Ответы
Автор ответа:
1
Ответ:
Применяем правила дифференцирования и таблицу производных .
Формула : .
Приложения:


Похожие вопросы
Предмет: География,
автор: fudjivara86
Предмет: Математика,
автор: eduardokramer001
Предмет: Литература,
автор: famm9117
Предмет: Английский язык,
автор: zotovd09
Предмет: Английский язык,
автор: polyakowakamilla