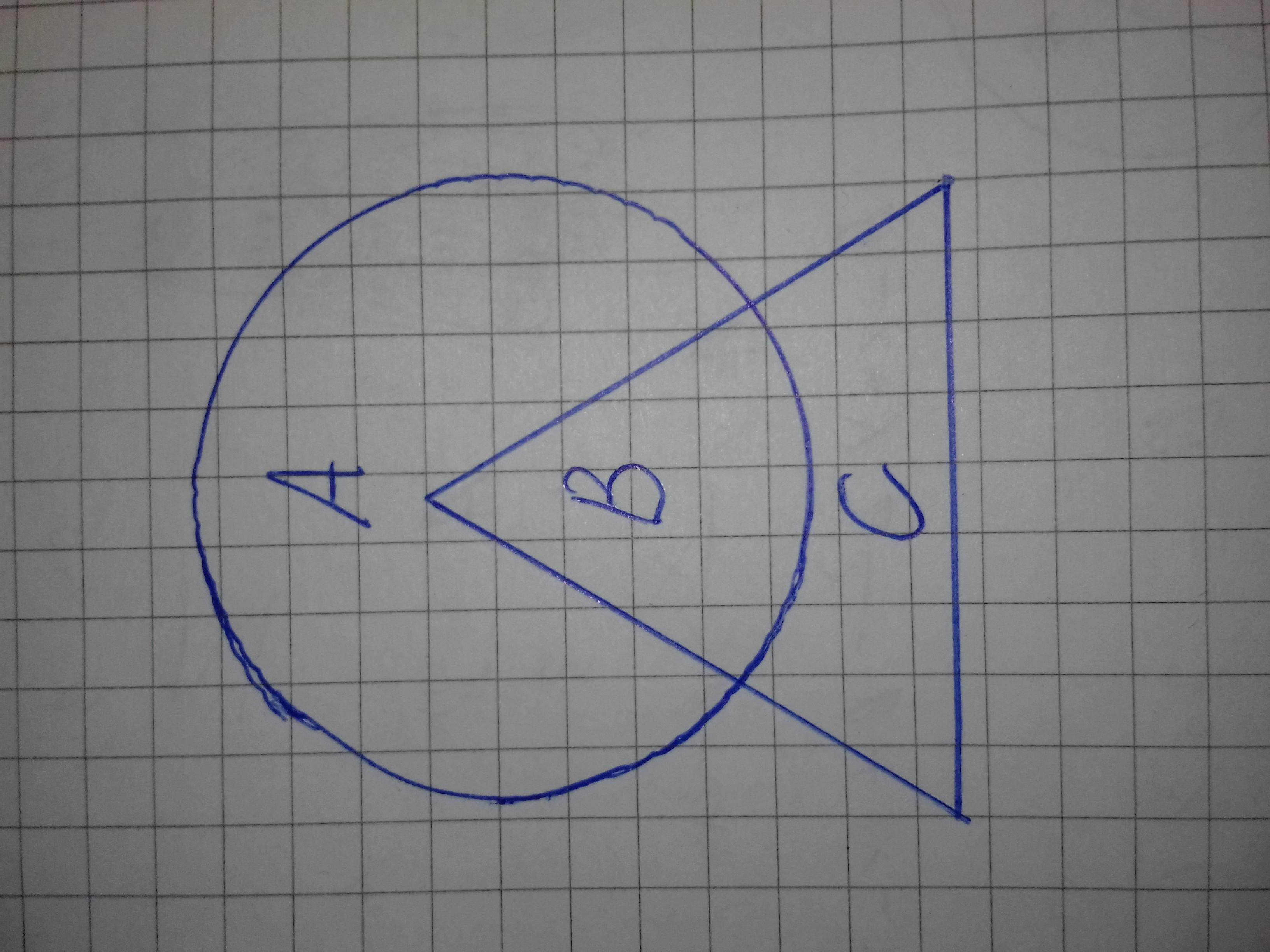
Трикутник і коло побудували таким чином, щоб вони перетинались, як це показано на малюнку. Відомо, що площа перетину фігур дорівнює 70% від їх обʼєднання, а площа частини кола, що не належить перетину, дорівнює 25% від їх перетину. Який відсоток площі трикутнику складає його частина, яка не належить перетину?
15%)
12%)
30%)
18%)
9%)
Ответы
Відповідь:
15% площі трикутнику складає його частина, яка не належить перетину.
Пояснення:
Позначимо як А - площу частини кола, що не належить перетину; як В - площу перетину кола та трикутника; як С - площу частини трикутника, яка не належить перетину.
1) Площа перетину фігур ( В ) дорівнює 70% від їх обʼєднання ( А + В + С ).
В = 70% / 100% × ( А + В + С )
В = 0,7 × ( А + В + С ) ( 1 )
2) Площа частини кола, що не належить перетину ( А ), дорівнює 25% від їх перетину ( В ).
А = 25% / 100% × В
А = 0,25 × В ( 2 )
3) Потрібно знайти який відсоток площі трикутника ( В + С ) складає його частина, яка не належить перетину ( С ).
С = Х% / 100% × ( В + С )
С = Х × 0,01 × ( В + С ) ( 3 )
4) Розкриємо дужки у рівнянні ( 1 ):
В = 0,7 × А + 0,7 × В + 0,7 × С
В - 0,7 × В = 0,7 × А + 0,7 × С
0,3 × В = 0,7 × А + 0,7 × С ( 4 )
5) З рівняння ( 2 ):
В = А / 0,25
В = 4 × А ( 5 )
6) Підставимо рівняння ( 5 ) до рівняння ( 4 ):
0,3 × 4 × А = 0,7 × А + 0,7 × С
1,2 × А - 0,7 × А = 0,7 × С
0,5 × А = 0,7 × С
А = 0,7 / 0,5 × С
А = 1,4 × С ( 6 )
7) Підставимо рівняння ( 6 ) до рівняння ( 5 ):
В = 4 × 1,4 × С
В = 5,6 × С ( 7 )
8) Підставимо рівняння ( 7 ) до рівняння ( 3 ):
С = Х × 0,01 × ( 5,6 × С + С )
С = Х × 0,01 × 6,6 × С
Х × 0,01 = С / ( 6,6 × С )
Х × 0,01 = 1 / 6,6
Х × 0,01 = 0,(15)
Х ≈ 15%