Предмет: Математика,
автор: zxcakumaqe
Обчислити границі функцій.
Приложения:
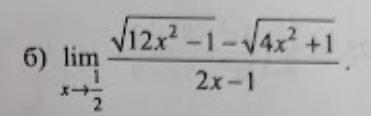
Ответы
Автор ответа:
0
Если мы подставим ½ вместо х, то получим неопределенность вида:
Поэтому воспользуемся правилом Лопиталя-Бернулли:
\displaystyle \lim_{x \to a } \frac{f(x)}{g(x)} = \lim_{x \to a} \frac{f'(x)}{g'(x)}
В нашем случае:
Для нахождения производной будем использовать следующие формулы:
Найдем производную f(x):
Найдем производную первого выражение (обозначим его за k(x)):
Пусть:
Тогда:
Сейчас найдем производную h(x):
Чтобы найти производную k(x) перемножим производную h(x) и k(h):
Найдем производную второго выражения (обозначим его за j(x)):
Пусть:
Тогда:
Найдем производную h(x):
Чтобы найти производную j(x) перемножим производную h(x) и k(h):
Следовательно:
Найдем производную g(x):
Сейчас найдем значение предела:
Ответ: √2
Похожие вопросы
Предмет: Литература,
автор: zlARCTIC
Предмет: История,
автор: VictoriaSenko
Предмет: Биология,
автор: yanok20080509
Предмет: Алгебра,
автор: NatsuLucy
Предмет: Математика,
автор: Mitrigo