Предмет: Математика,
автор: dudunya3521
Ради всего святого!!!!!
Срочноо
Приложения:
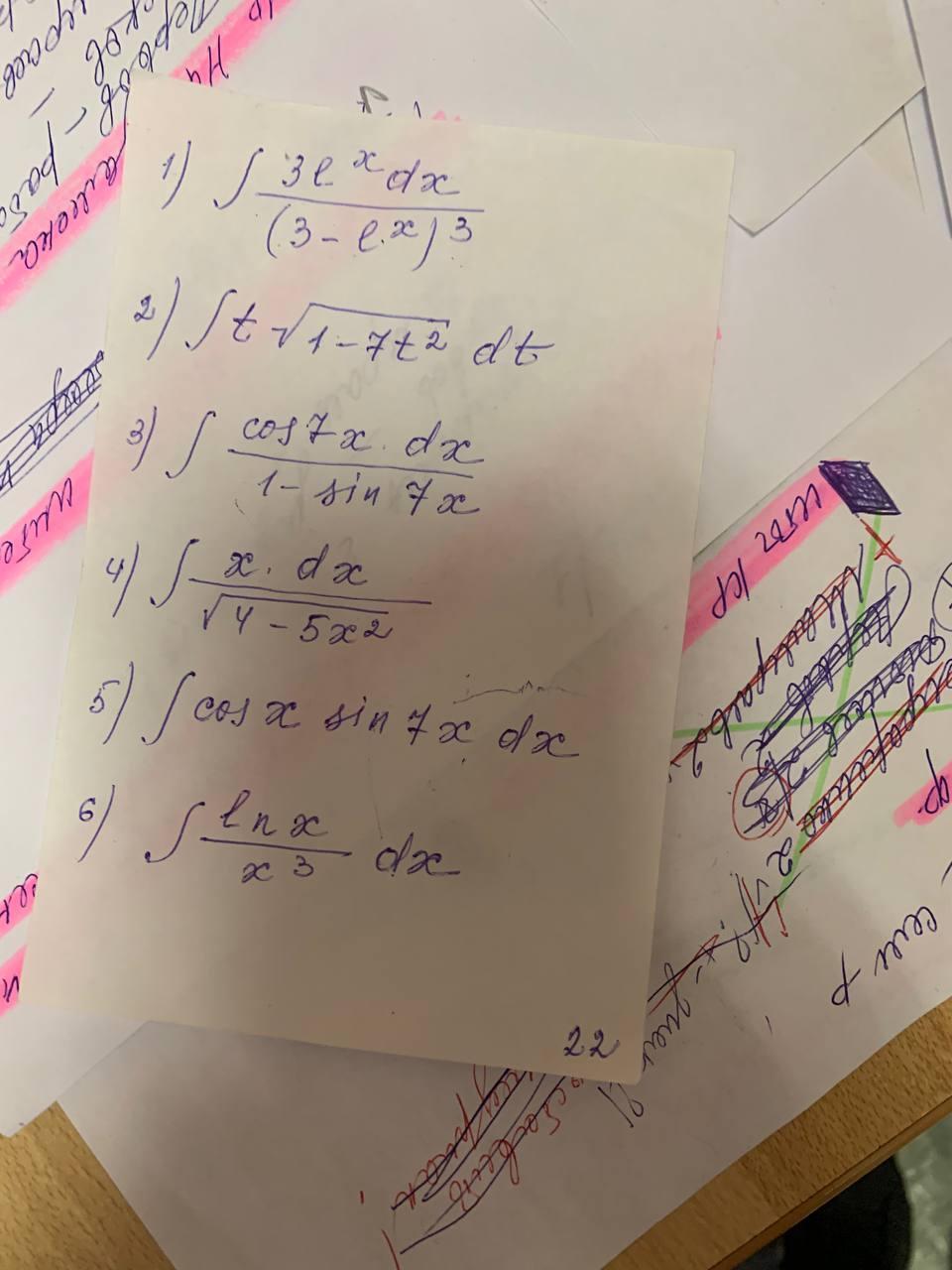
Ответы
Автор ответа:
2
Ответ:
Пошаговое объяснение:
Вычислить интегралы:
Замена переменной:
3 - еˣ = t
-eˣdx = dt ⇒ eˣdx = -dt
Получим:
Обратная замена:
Замена переменной:
1 - 7t² = x
-14t dt = dx
t dt = -dx/14
Получим:
Обратная замена:
Замена переменной:
1 - sin 7x = t
-7 cos 7x dx = dt
cos 7x dx = -dt/7
Получим:
Обратная замена:
Замена переменной:
4 - 5x² = t
-10x dx = dt
x dx = -dt/10
Получим:
Обратная замена:
- Воспользуемся формулой:
2sinα cosβ = sin(α + β) + sin(α - β)
- Интегрирование по частям:
∫u dv = uv - ∫v du
#SPJ1
Приложения:
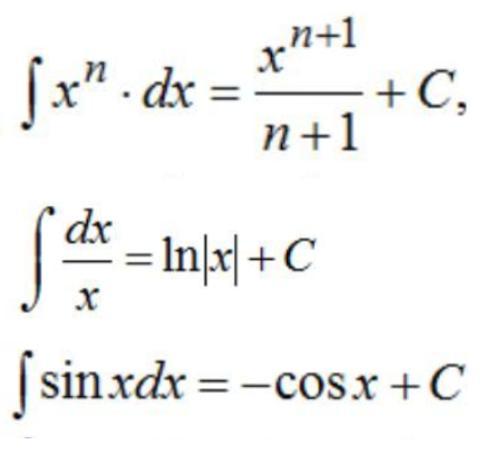
dudunya3521:
Я вас люблю, спасибо вам большое!!!!!
Похожие вопросы
Предмет: Математика,
автор: timilchenko12
Предмет: Алгебра,
автор: tronevihs
Предмет: Другие предметы,
автор: jekrkrkr
Предмет: Право,
автор: katchiev010