Предмет: Математика,
автор: finix31
срочно помогите пожалуйста
Приложения:
Ответы
Автор ответа:
0
Ответ:
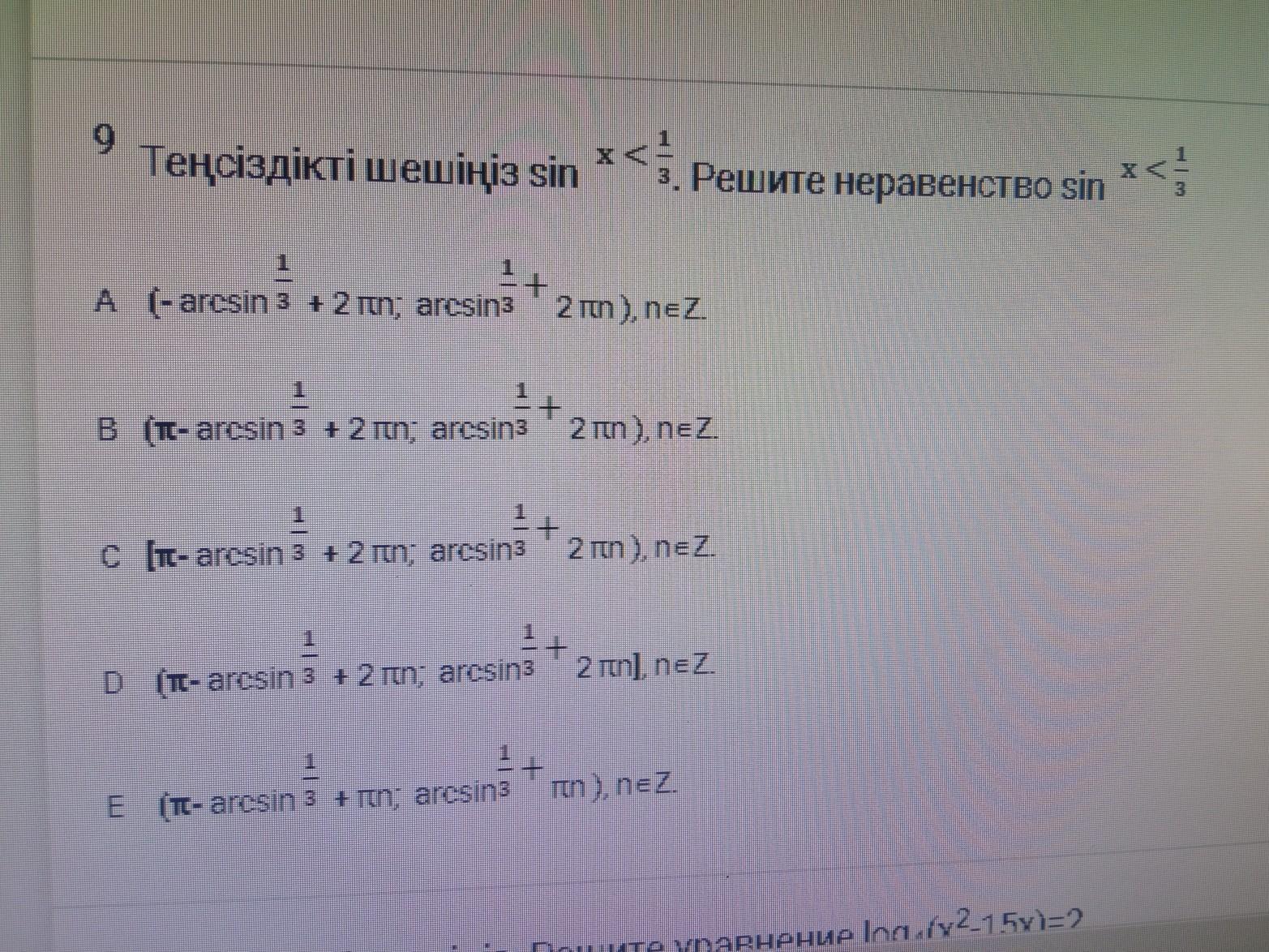
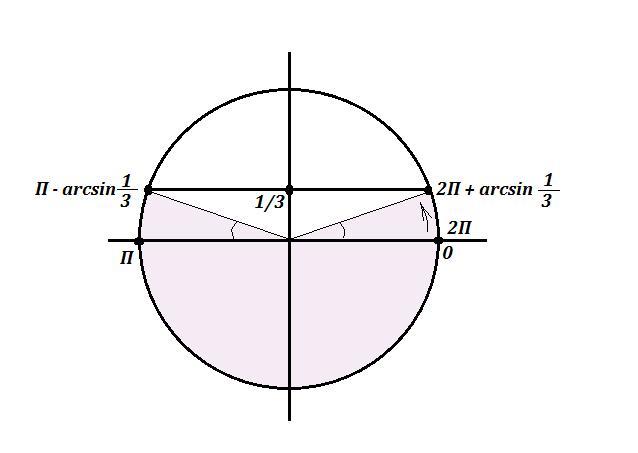
Решить неравенство : .
Если , то
Тогда решением неравенства будут значения х такие, что выполняется неравенство
Ответ:
Приложения:

Похожие вопросы
Предмет: Українська мова,
автор: uzdanadia34
Предмет: Математика,
автор: v56433017
Предмет: Математика,
автор: olganekotan
Предмет: Математика,
автор: fat300984