Предмет: Алгебра,
автор: saurbaevdulat593
Найдите наибольшее и наименьшее значения функции на отрезке:
f(x)=x^3-3x^2-9x+23; [-4;4]
Ответы
Автор ответа:
0
Ответ:
f(x)=x^3-3x^2-9x+23;
f'(x)=(x^3-3x^2-9x+23)' = 3x²-6x-9 {:3} = x²-2x-3.
Находим корни уравнения
x²-2x-3=0.
По т. Виета
x1+x2=2;
x1*x2=-3;
x1=-1;
x2=3.
Точки экстремума x1=-1; x2=3.
MAX => f(-1) = (-1)³-3(-1)²-9(-1)+23 = 28.
MIN => f(3) = (3)³-3(3)²-9(3)+23 = -4.
Приложения:

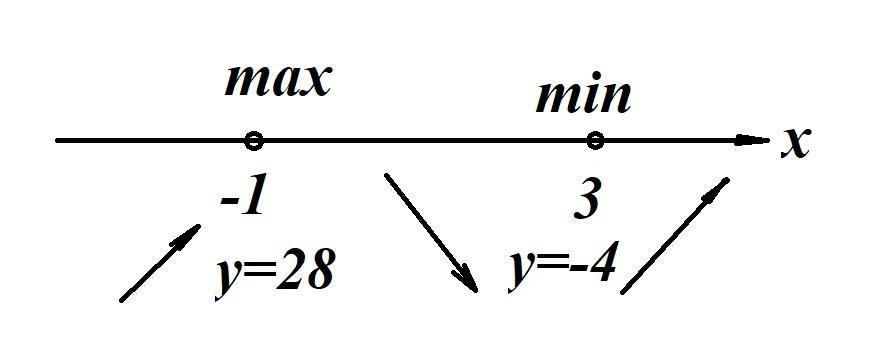
Автор ответа:
0
Ответ: у min = - 53 ; y max = 28
Похожие вопросы
Предмет: История,
автор: katerinakasacka
Предмет: Математика,
автор: vitausin4
Предмет: Другие предметы,
автор: 234565678901az
Предмет: Математика,
автор: mrvladkovalev99
Предмет: Информатика,
автор: ivanow38