Предмет: Математика,
автор: katygreyf2005
50 баллов, Найти пределы
Приложения:
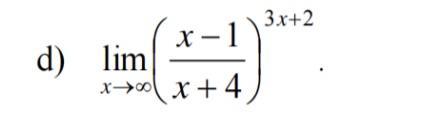
Ответы
Автор ответа:
1
Ответ:
(см. объяснение)
Пошаговое объяснение:
Задание выполнено!
Похожие вопросы
Предмет: География,
автор: maranacupinka26
Предмет: Биология,
автор: ze240946
Предмет: Математика,
автор: tarassmetanka44
Предмет: Математика,
автор: uuuedfdsf
как минимум это нескромно, как максимум - мания величия.