Предмет: Алгебра,
автор: ymnyichel2009
Найти площади фигур ограниченные следующими линиями:

Simba2017:
S=интеграл(17-17x^2) dx , пределы интегрирования от -1 до 1
S=74/3
Ответы
Автор ответа:
0
Объяснение:
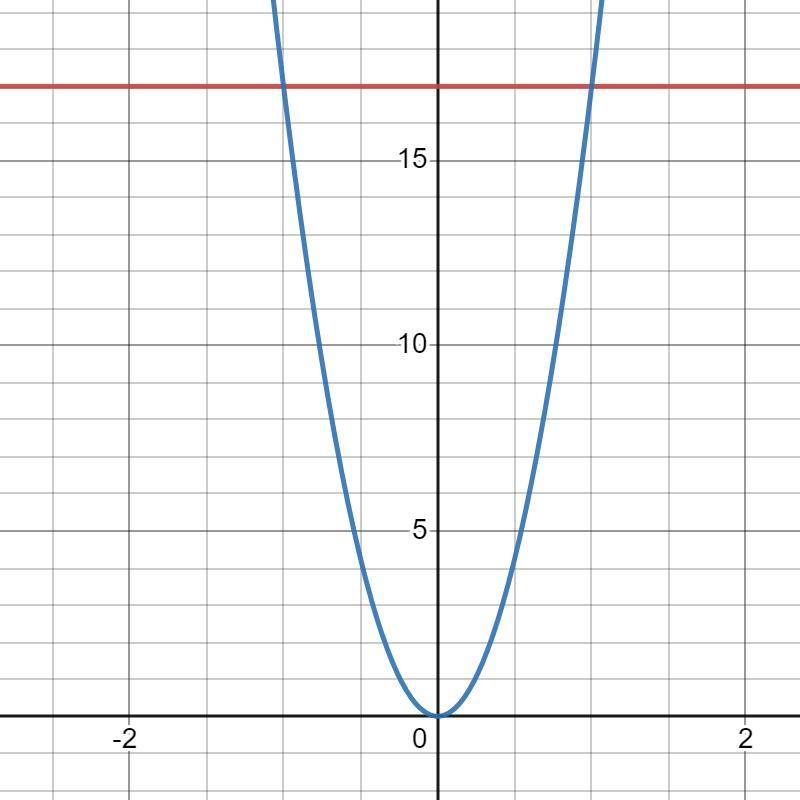
y=17 y=17x² S=?
17x²=17 |*17
x²=1
x²-1²=0
(x+1)*(x-1)=0
x₁=-1 x₂=1 ⇒
Ответ: S≈22,666667 кв. ед.
Приложения:
Похожие вопросы
Предмет: Немецкий язык,
автор: eliseykachica
Предмет: Литература,
автор: lyntik590
Предмет: Литература,
автор: rotory4
Предмет: Алгебра,
автор: tonyamulik
Предмет: Математика,
автор: DirolWhite