Предмет: Математика,
автор: podsjgosjdgphsd
Решить уравнение..................
Приложения:
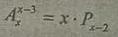
Ответы
Автор ответа:
1
Произведение равно 0, когда 1 из множителей равен 0, следовательно:
(x-2)! = 0 решений не имеет, т.к. левая часть всегда положительна
Проверка:
Неверно
Верно
Ответ: x = 7
Похожие вопросы
Предмет: Українська мова,
автор: yurdaria988
Предмет: Физика,
автор: fingerscccut
Предмет: Алгебра,
автор: halafmiroslava
Предмет: Алгебра,
автор: AntonLyagin1