Предмет: Математика,
автор: vasfasihgiaosg
Вычислить площадь плоской фигуры, ограниченной линиями
Приложения:
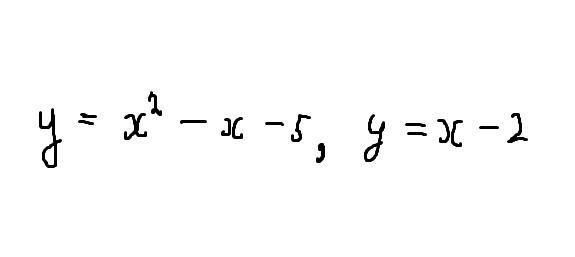
Ответы
Автор ответа:
0
Ответ: 56/3 кв. ед.
Пошаговое объяснение:
Строим графики функций y=x^2-x-5; y=x-2.
S=∫ₐᵇ(f₁(x)-f₂(x))dx;
Пределы интегрирования находим по графикам функций
a=-1; b=3 или решив уравнение
x^2-x-5 = x-2;
x^2-2x-3=0.
По т. Виета
x1+x2=2;
x1*x2=-3;
a=x1=-1;
b=x2=3.
Тогда
S=-∫₋₁³(x-2)dx - ∫₋₁³(x^2-x-5)dx = 44/3 + 4 = 56/3 кв. ед.
1) ∫₋₁³ -(x-2)dx = -∫₋₁³(x)dx + ∫₋₁³2dx = - 1/2(x²)|₋₁³ + 2(x)|₋₁³ =
= - 1/2(3²-(-1)²) + 2(3-(-1)) = -1/2*8 + 2*4 = -4 + 8 = 4 кв.ед.
2) -∫₋₁³(x^2-x-5)dx = -1/3(x^3)|₋₁³+1/2(x^2)|₋₁³ + 5(x)|₋₁³ =
= -1/3(3³-(-1)³) + 1/2(3²-(-1)²) + 5(3-(-1)) = -1/3*28 + 1/2*8 + 5*4=
= -28/3 + 4+20 = -28/3 + 24 = 44/3 кв. ед.
Приложения:

Похожие вопросы
Предмет: Математика,
автор: erikbro2912
Предмет: Українська мова,
автор: pupumaska
Предмет: Английский язык,
автор: dilshodbekumurzakov3
Предмет: Математика,
автор: dimoksitnikov08