Предмет: Математика,
автор: gradients51
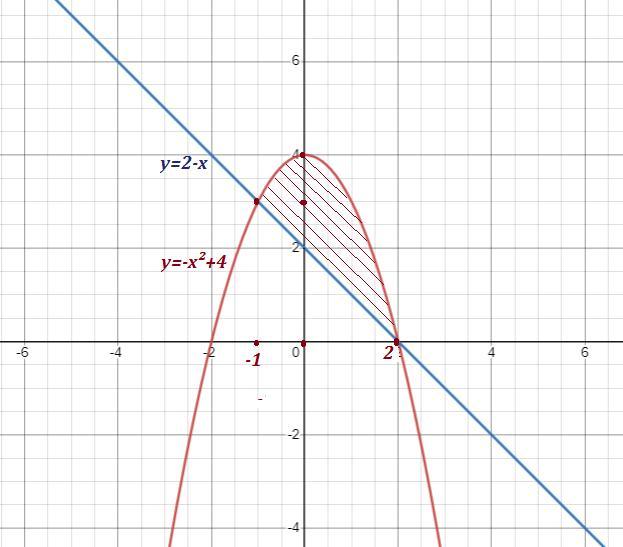
Вычислить площадь плоской фигуры ограниченной линиями
Приложения:

Ответы
Автор ответа:
0
Ответ:
Плоская фигура ограничена параболой и прямой
Точки пересечения линий :
Приложения:
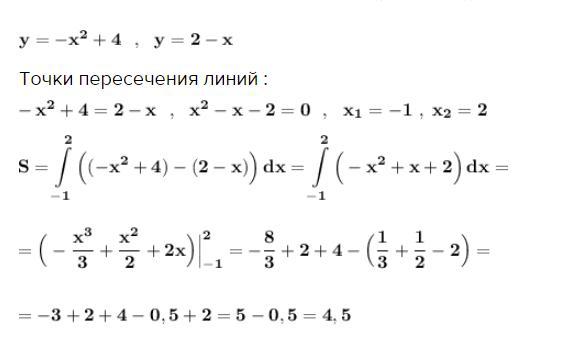
Похожие вопросы
Предмет: Українська мова,
автор: uzdanadia34
Предмет: Математика,
автор: v56433017
Предмет: Математика,
автор: olganekotan
Предмет: Алгебра,
автор: kimajan666
Предмет: Физика,
автор: mashapleskun2706