Предмет: Математика,
автор: ChocolatePiggy08
Вычислите площадь S фигуры, заданной на плоскости системой неравенств (см. прикрепленное фото).
Тогда значение выражения 4S/x равно — ?
Приложения:
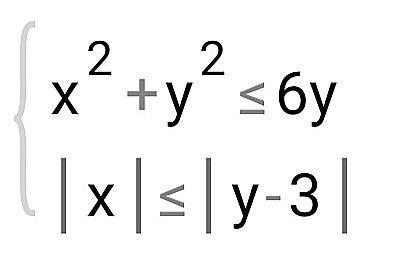
Ответы
Автор ответа:
1
Ответ:
4.5π
Пошаговое объяснение:
1) Найдем площадь фигуры, образованной первой формулой.
Эта фигура является кругом(не окружность) с радиусом 3(3^2=9 - справа) центр которой в (0;3). Ее площадь равна:
2) Найдем площадь фигуры образованной системой:
Подставим x=0, y=3 - координаты центра круга - во вторую формулу и получим |0|=|0|. Значит площадь фигуры пересечения равна 1/2*s=4.5π
ChocolatePiggy08:
Спасибо!
Пожалуйста
пж отметь лучшим
Похожие вопросы
Предмет: География,
автор: anna88lobanova
Предмет: Українська мова,
автор: ulianka2445
Предмет: История,
автор: angelinaargirova11
Предмет: Математика,
автор: alonasmislaeva181
Предмет: Геометрия,
автор: belouskata992